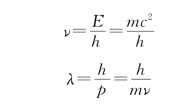12.5 粒子的波动性
1924年,法国博士研究生德布罗意在光的波粒二象性的启发下想到,自然界在许多方面都具有明显地对称性,如果光具有波粒二象性,则实物粒子,如电子,也应该具有波粒二象性。于是,他大胆地在他的博士论文中提出假设:实物粒子也具有波动性。他把光子的能量-频率和动量-波长的关系式借鉴来,提出一个粒子的能量E和动量p跟与它相联系的波的频率ν和波长λ的定量关系与光子的一样,即

应用于粒子的这些公式后来被称为德布罗意公式,和粒子相联系的波称为物质波或德布罗意波,式(12.12)给出了相应的德布罗意波长。德布罗意是采用类比法提出他的假设的,当时并没有任何直接的证据。但他的假设提出不久就得到了实验证实,并且直接引发了一门新的理论——量子力学——的建立。
1927年,戴维孙和革末做了电子束在晶体表面上散射的实验,观察到了和X射线衍射类似的电子衍射现象,首先证实了电子的波动性。同年,汤姆孙做了电子束穿过多晶薄膜的衍射实验(图12.8),成功地得到了和X射线通过多晶薄膜后产生的衍射图样极为相似的衍射图样(图12.9)。1961年,约恩孙做了电子的单缝、双缝、三缝等衍射实验,得出的明暗条纹更加直接地证实了电子具有波动性。
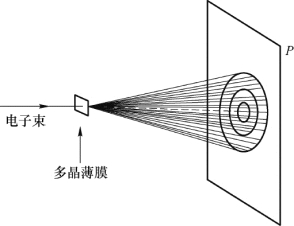
图12.8 汤姆孙电子衍射实验简图

图12.9 电子衍射图样
除了电子以外,之后还陆续通过实验证实了中子、质子、原子甚至分子都具有波动性,德布罗意公式对这些粒子同样适用。这就说明一切微观粒子都具有波粒二象性,德布罗意公式就是描述微观粒子波粒二象性的基本公式。
粒子的波动性有很多重要的应用。例如,由于低能电子波的穿透深度较X光小,所以低能电子衍射被广泛地用于固体表面性质的研究。由于中子易被氢原子散射,所以中子衍射就被用来研究含氢的晶体。电子显微镜利用了电子的波动性,由于电子的波长可以很短,电子显微镜的分辨能力可以达到0.1 nm。
![]()
1.黑体辐射
维恩公式为
![]()
瑞利-金斯公式为
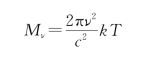
普朗克黑体辐射公式为

能量子为
E=hν
普朗克常量为(https://www.daowen.com)
h=6.626 075 5×10-34 J·s
2.光电效应
光电子逸出时的最大初动能和截止电压U c的关系应为
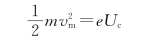
光电效应方程为
![]()
红限频率为
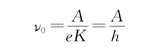
3.光的波粒二象性
光子的能量为
E=hν
光子的质量为
![]()
光子的动量为
4.康普顿散射
康普顿散射公式为
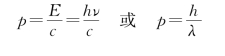
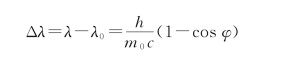
5.粒子的波动性
德布罗意公式为