10.3.2 理想气体的压强
宏观上所测量到的气体施与容器壁上的压强,是大量气体分子对容器壁不断碰撞的结果。因为就单个分子来说,它在什么时候,以多大冲击力,碰在器壁什么地方都是偶然的。但由于分子的数量巨大,而它们对器壁的碰撞又是极其频繁的,因此在我们观测的时间d t内(例如d t=1 s,这对微观粒子的运动来说,时间已足够长了),仪器感受不到个别分子冲力的瞬时变化,只记录到大量分子的综合平均冲力

因此,气体的压强等于大量分子在单位时间内施加在单位器壁面积上的平均冲量。这一平均冲量可通过器壁的反作用所引起的大量分子的总动量变化求得。
设在体积为V的容器中有理想气体,它由N个质量为m的分子组成。在平衡态下,器壁各处压强相等,所以我们可以在器壁上任选一面积元d A,d A垂直于x轴(如图10.3所示)。
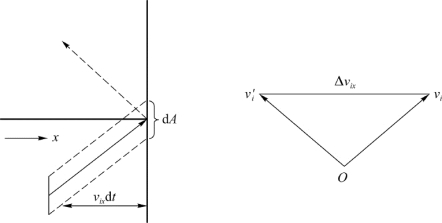
图10.3 速度为vi的分子对d A碰撞引起的动量变化
为简单起见,设分子与器壁的碰撞是完全弹性的,因此碰撞前后分子速度沿器壁切线方向分量没有改变,法线分量由v x变为-v x。根据动量定理,速度为v i的分子撞击器壁后,由于器壁给予分子的反冲量而引起分子的动量改变量为
![]()
方向向左。因此,分子施于器壁的冲量的大小为2mv ix,方向向右。
设容器中速度沿x方向分量v ix(严格来说在v ix附近)的分子数目是N i,则在d t时间内来得及与d A发生碰撞的分子就是那些与右壁的垂直距离为v ix d t,并向右壁前进的分子,如图10.3所示,即那些位于以d A为底、v ix d t为高,其母线为v ix d t的斜柱体内的那部分分子。这些分子的数目是(https://www.daowen.com)

把式(10.16)对具有各种可能速度分量v ix的分子求和,就得到全体分子作用在右壁d A上的总的动量变化,它应等于全体分子作用在d A上的总冲量。
![]()
因为平均说来,全体分子约有一半向左运动(vix<0),另一半向右运动(v ix>0),而向左运动的一半是不必考虑的,因此累加号前乘1/2。将式(10.17)代入式(10.13),则气体的压强为
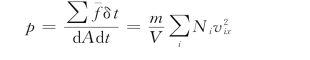
由式(10.10)得
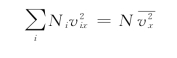
所以
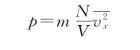
由式(10.11)得
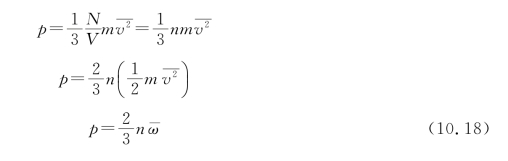

从微观角度来说,气体压强这个概念具有统计的意义。在计算中所用到的d A与d t都是从宏观上看很小而从微观上看很大的量,因此,在d t时间内撞击d A面积上的分子数是大量的。所以压强公式的推导是从对大量分子的冲量求统计平均的概念出发,应用了大量分子在各方向运动机会均等这一统计假设,最后求得压强的统计平均值。因此,压强公式是用普遍的力学原理结合简单的统计概念和方法所得出的一个统计规律。它指出,宏观量压强p是相应分子的微观量v 2的统计平均值,气体的压强是大量分子碰撞所产生的宏观效应。说某个分子的压强如何是没有意义的,单个分子虽服从力学规律,大量分子无规则运动的整体却服从统计规律。
