3.3.2 质心运动定理
由质心的位置矢量公式:
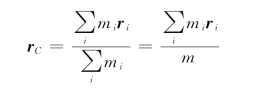
两边对时间求导,可得质心运动的速度为
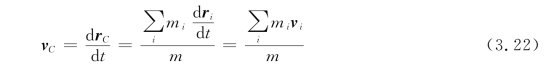
即因此,质点系的总动量等于质点系的总质量与质心的运动速度之积,即质心的动量p C。由质点系的动量定理即式(3.15)可知


式(3.26)即为质心运动定理(质点系的牛顿第二定律):作用在一个质点系的合外力等于系统总质量与质心加速度之积。
由质心运动定理知,质心的运动等同于一个质点的运动,这个质点具有质点系的总质量,它所受的外力是质点系所受的所有外力的和。它告诉我们,无论系统内各质点的运动如何复杂,质心的运动可能都相当简单,只由外力的矢量和决定,内力不会影响质心的运动状态。
若外力矢量和为零,则质心速度不变,则系统的总动量守恒,即
![]()
而
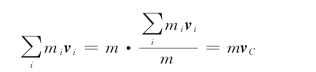
由此可得到动量守恒定律的另一种表述形式:当质点系不受外力或所受外力矢量和为零时,系统的质心保持静止或匀速直线运动。它通常被用来求解距离问题,如下面的两个例题。
例3.8 设有一质量为2 m的弹丸从地面斜抛出去,它飞行在最高点处爆炸成质量相等的两个碎片,如图3.11所示,其中一个碎片竖直下落,另一碎片水平抛出,它们同时落地,试问第二个碎片落地点在何处?
解 考虑弹丸为一系统,空气阻力略去不计。设m 1和m 2为第一个和第二个碎片的质量,且m 1=m 2=m;x 1和x 2为两碎片落地时距原点O的距离,x C为两碎片落地时它们的质心距原点O的距离。由图3.11可知x 1=0,于是可得
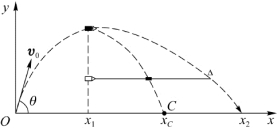
图3.11 例3.8用图
![]()
由于m 1=m 2=m,所以由上式有
x 2=2x C(https://www.daowen.com)
即第二个碎片的落地点与第一个碎片的落地点的水平距离为碎片的质心与第一个碎片水平距离的两倍。
例3.9 如图3.12所示,质量为m 1=50 kg的人站在一条质量m 2=350 kg、长L=5.6 m的船头,开始时船静止。忽略水的阻力,试求当人走到船尾时船移动的距离。
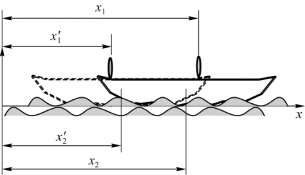
图3.12 例3.9用图
解 水平方向不受力,质心速度不变,即在人从船头走到船尾过程中系统质心的位置不变。设船向左移动d,人在船头时
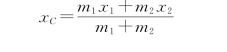
人在船尾时
![]()
联立上面两式得
m 1(x′1-x 1)=m 2(x 2-x′2)
又由相对运动的位移变换式
![]()
得
x′1-x 1=L+(x′2-x 2)=L-d
代入上面的公式可得
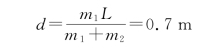
质心运动定理体现了“质心”这一概念的重要性。这一定理告诉我们,一个质点系内各个质点由于内力和外力的作用,运动情况可能很复杂,但相对于此质点系有一个特殊的点,即质心,它的运动可能相当简单,只由质点系所受的合外力决定。例如,一颗手榴弹可以看作一个质点系。投掷手榴弹时,将看到它一边翻转,一边前进,其中各点的运动情况相当复杂。但由于它受的外力只有重力(忽略空气阻力的作用),它的质心在空中的运动却和一个质点被抛出后的运动一样,其轨迹是一个抛物线。又如,高台跳水运动员离开跳台后,他的身体可以做各种优美的翻滚伸缩动作,但是他的质心却沿着一条抛物线运动(图3.13)。
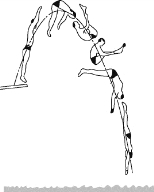
图3.13 跳水运动员
此外,我们知道,当质点系所受的合外力为零时,该质点系的总动量保持不变。由式(3.26)可知,该质点系质心的速度也将保持不变。因此,系统的动量守恒定律也可以表述为:当一质点系所受的合外力等于零时,其质心速度保持不变。
需要指出的是,在这以前我们常常用“物体”一词来代替“质点”。在某些问题中,物体并不能当成质点看待,但我们还是用了牛顿定律来分析研究它们的运动。严格来说,我们是对物体用了式(3.26)所示的质心运动定理,而所分析的运动实际上是物体质心的运动。在物体做平动的条件下,因为物体中各质点的运动相同,所以完全可以用质心的运动来代表整个物体的运动。
