10.1.2　概率

以伽尔顿板实验为例,设小球总数为N,落入第i个狭槽的小球数为ΔN i,当小球总数N很大时,我们定义小球落入第i个狭槽概率为

小球落入第i个狭槽是偶然事件,偶然事件出现的概率就是在一定条件下,该事件出现的可能性大小的量度。就是说,单个小球投入之后,无法预言小球是否落入第i个狭槽,大量小球投入,小球落入第i个狭槽的可能性用落入该槽的小球数ΔN i与投入小球总数N的比值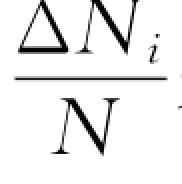来 量度。落入该槽的小球数占小球总数的百分比越大,小球落入该槽的可能性也越大,也即小球落入该槽的概率越大。在伽尔顿板实验中,小球数目按狭槽位置的分布曲线,如图10.1(b)所示。

假设伽尔顿板共有n个狭槽,小球落入各个狭槽的概率分别为P 1,P 2,…,Pi,…,Pn,小球落入所有狭槽的概率之和或总概率应等于1,即

式(10.2)称为归一化条件,概率分布满足归一化条件。