11.2.1 功
在力学中,把物体所受的力F和物体在力的作用线上的位移d l的标积定义为力所做的功,即
d A=F·d l
而且,做功是物体与外界交换能量的过程,做功的结果使物体的运动状态发生变化。
在热力学中,准静态过程的功可直接利用系统的状态参量来计算。最常见的是和系统体积变化相联系的机械功,如图11.3所示。
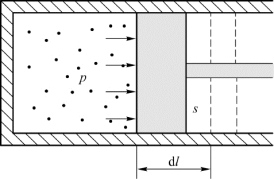
图11.3 气体膨胀时做功的计算
设气缸内气体准静态膨胀,以S表示活塞的面积,以p表示气体的压强。气体对活塞的压力表示为p S,当气体推动活塞向外缓慢地移动一段微小位移d l时,气体的体积也增加了一微小量d V,这时气体对外界做的元功d A为
元功d A表示在一个无限小过程所做的功的量值,不表示全微分。
当系统膨胀(d V＞0)时,d A为正,系统对外界做功;当系统被压缩(d V＜0)时,d A为负,系统对外界做负功,实际上是外界对系统做功。
当系统经历一有限的准静态过程,体积由V 1变化到V 2时,系统对外做的总功为
式(11.1)及式(11.2)具有普遍性。对于任一系统,只要做功是通过体积变化来实现的,而且所进行的是准静态过程,其他功和总功都可以分别由此两式表示。
系统的准静态过程可以方便地在p-V图上表示出来,膨胀过程的功为正值,而压缩功为负值。如图11.4中(a)和(b)所示,曲线ab表示某一准静态过程,小矩形面积数值上等于系统做的元功,而曲线下的总面积数值上等于系统在这一过程中做的总功。
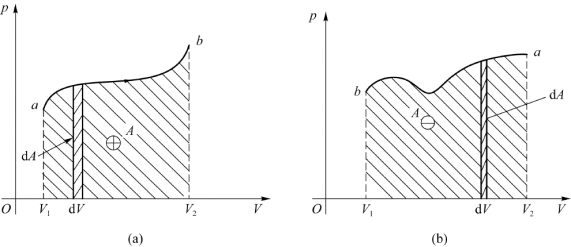
图11.4 体积功等于p-V曲线下的面积
从图11.4中可以看出,功的大小不仅与始末状态有关,而且与所经历的过程有关。这就是说,即便始末状态已定,还要根据两状态间的具体过程曲线的形状(即过程中压强随体积变化的函数关系)才能确定功的值。所以,功不是表征系统状态的量,而是与做功过程有关的过程量。也就是说,式(11.1)所表示的元功d A并不是A在数学上的全微分。因此,我们不能说“系统的功是多少”或“处于某一状态的系统有多少功”,而只能说“系统通过某一过程做了多少功”。