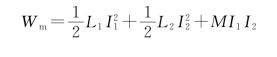8.5 磁场的能量
在图8.16(b)所示的实验中,当开关K打开后,电源已不再向灯泡提供能量了,它突然强烈地闪亮一下所消耗的能量是哪里来的呢?由于使灯泡闪亮的电流是线圈中的自感电动势产生的电流,而该电流随着线圈中磁场的消失而逐渐消失,所以可以认为使灯泡闪亮的能量是原来储存在通有电流的线圈中的,或者说是储存在线圈内的磁场中的。因此,这种能量叫作磁能。自感为L的线圈中通有电流I时所储存的磁能应该等于该电流消失时自感电动势所做的功。这个功可如下计算。以i d t表示在短路后某一时间d t内通过灯泡的电量,则在这段时间内自感电动势所做的功为
电流由起始值减小到零时,自感电动势所做的总功为
因此,自感为L的线圈通有电流I时所具有的磁能为
这就是自感磁能公式。
对于磁场的能量也可以引入能量密度的概念,下面我们用特例导出磁场能量密度的公式。
考虑一个螺绕环,在例8.5中,已求出螺绕环的自感系数为
L=μn 2V
利用式(8.29)可得通有电流I的螺绕环的磁场能量是
由于螺绕环管内的磁场B=μnI,所以上式可写作
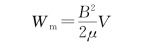
由于螺绕环的磁场集中于环管内,其体积为V,并且管内磁场基本上是均匀的,所以环管内的磁场能量密度
利用磁场强度H=B/μ,此式还可以写成
式(8.31)虽然是从一个特例中推出的,但是可以证明它对磁场普遍有效。利用它可以求得某一磁场所存储的总能量为
此式的积分应遍及整个磁场分布的空间。
例8.9 求两个相互邻近的电流回路的磁场能量,这两个回路的电流分别是I 1和I 2。
解 两个回路如图8.19所示。为了求出此系统在所示状态时的磁能,我们设想I 1和I 2是按下述步骤建立的。
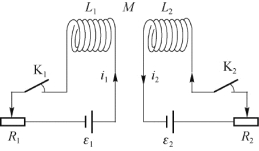
图8.19 图8.9用图(两个载流线圈的磁场能量)
(1)先合上开关K 1,使i 1从0增大到I 1。这一过程中由于自感L 1的存在,由电源ε1做功而储存到磁场中的能量为
由于这两种通电方式下的最后状态相同,即两个电路中分别通有I 1和I 2的电流,那么能量应该与达到此状态的过程无关,也就是应有W m=W′m。由此我们得
M 12=M 21
即回路1对回路2的互感系数等于回路2对回路1的互感系数。用M来表示此互感系数,则最后储存在磁场中的总能量为
