3.5.1 质点系的角动量定理
2026年01月14日
3.5.1 质点系的角动量定理
上述针对单个质点得到的角动量定理还可以推广到多个质点构成的质点系中去。如图3.24所示,设有n(n=1,2,…)个质点构成质点系,质点系的角动量为系统中各质点对同一参考点(坐标原点)的角动量的矢量和:
![]()
作用于质点系各质点的力可分为外力和内力。外力形成外力矩,内力形成内力矩,合力矩为外力矩和内力矩(对同一参考点)的矢量和。
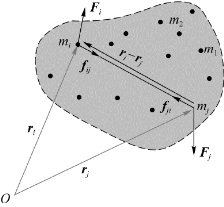
图3.24 质点系的角动量定理
现在考虑质点系中第i个质点,该质点受到的合力矩M i=M外i+M内i,角动量为L i,由质点的角动量定理有
![]()
质点系有n个质点,i=1,2,…n,一共可以列出n个这样的方程,现在对这n个方程求和:
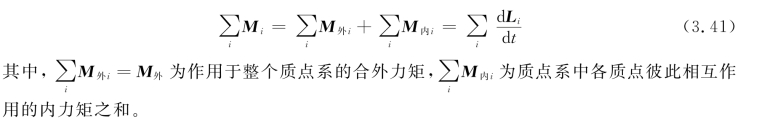 (https://www.daowen.com)
(https://www.daowen.com)
如图3.24所示,一对内力f ij和f ij(=-f ji)的力矩和为

这就是质点系的角动量定理:作用于质点系的合外力矩等于质点系对同一参考点的角动量对时间的变化率。
也可以将式(3.44)改写为微分形式:
![]()
考虑从t 1时刻到t 2时刻,质点系角动量从L 1变化到L 2,对式(3.45)积分得
![]()
等号左侧的积分是合外力矩对时间的累积,即冲量矩,等号右侧L 1-L 2=ΔL是相同时间内质点系角动量的增量,这是与式(3.44)相对应的质点系的角动量定理的积分形式。
式(3.45)和式(3.46)都说明只有作用于系统的合外力矩才改变系统的角动量,内力矩并不改变系统的角动量。内力矩起的作用只是在系统内各质点间彼此交换角动量。这个规律与质点系的动量定理相似。
