4.3.4 势能
从上面关于万有引力、重力和弹力做功的讨论中我们知道,这些保守力做功均只与系统的始末位置有关,为此,可以引入一物理量,它是位置的函数,我们把这种与系统相对位置(一般称作位形)有关的能量定义为系统的势能或势函数,用E p表示。这样,与初态位形相关的势能用E p a表示,与末态位形相关的势能用E p b表示,重力做功、弹力做功、万有引力做功就可以归纳成
![]()
式(4.22)为势能的定义式,即保守力对物体做的功等于物体势能增量的负值,该表述也被称为势能定理。由此可知,势能的绝对值是没有物理意义的,只有势能差才有物理意义。势能是由系统相互作用力和系统的位形(相对位置)决定的能量,因此势能只能是一个相对值,要确定系统处于某一位形(通常简称为物体在空间某点)的势能,需要选择一个参考位形(简称为参考点),叫作势能零点,可用r 0表示,势能零点的势能E p(r 0)=0。现在利用势能定理,令b为势能的零点,E p b=0,a为任意一点,位形为r,则
![]()
式(4.23)是势能计算的普遍公式,根据这个公式,空间某点(某位形)的势能等于保守力由该点(r)到势能零点(r 0)的功。
一个复杂的系统可能包含有不止一种势能。例如,一个竖直悬挂的弹簧振子就既有重力势能,又有弹性势能。这时可以把各种势能的总和定义为系统的势能,势能定理依然成立。
于是,三种势能分别为
·重力势能(https://www.daowen.com)
E p=mgh
·引力势能

·弹性势能
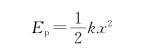
同重力势能一样,万有引力势能和弹性势能也是与势能零点选取有关的。显然,上述公式表示的万有引力势能的零点在两个质点的距离为无限大时(r=∞),弹性势能的零点对应弹簧的原长,重力势能的零点为y=0处。当然,势能零点也可以任意选取,选取不同的势能零点,物体的势能就将具有不同的值。势能可正可负,势能为负表明其势能大小比选作零点的势能小。所以,通常说势能具有相对意义。但也应当注意,任意两点间的势能之差却是具有绝对性的。
势能是属于系统的。势能是由于系统内各物体间具有保守力作用而产生的,因而它是属于系统的。单独谈单个物体的势能是没有意义的。例如,重力势能就是属于地球和物体所组成的系统的。如果没有地球对物体的作用,也就谈不上重力做功和重力势能的问题,离开了地球作用范围的宇宙飞船,也就无所谓重力势能。同样,弹性势能和引力势能也是属于有弹性力和引力作用的系统的。应当注意,在日常叙述时,常将地球与物体系统的重力势能说成物体的,这只是为了叙述上的简便,其实它是属于地球和物体系统的。物体的引力势能和弹性势能也都是这样。
