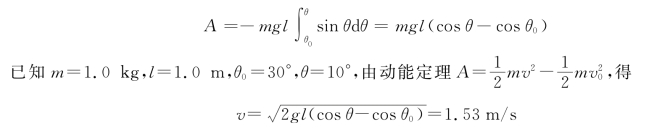4.2.1　质点的动能定理

4.2.1　质点的动能定理

如图4.6所示,质量为m的物体在力F的作用下由A到B,速度由v 1到v 2,元功为

由牛顿第二定律及切向加速度a t的定义

又

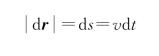
所以

质点自A到B这一过程中,合外力所做的总功为

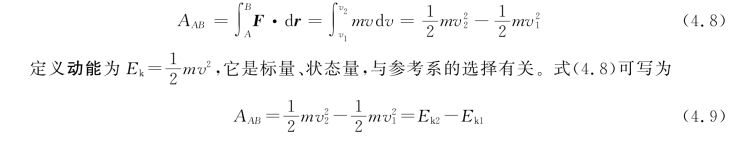
合外力对质点所做的功等于质点动能的增量,这就是质点的动能定理。

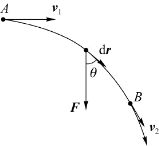
图4.6　动能定理

动能是机械能的一种形式,是由于物体运动而具有的一种能量。动能的单位与功相同,但意义不一样。功是力的空间累积,与过程有关,是过程量;动能则取决于物体的运动状态,或者说是物体机械运动状态的一种表示,因此是状态量,也称为态函数。

质点系的动能定义为系统中各个质点动能之和(代数和)。数学表达式为

我们可以看到,研究对象的总动能常用E k表示,而对系统中各个质点的动能则使用下标i来区分。由于动能与物体运动速度有关,一般来讲不同时刻质点或系统的动能是不同的,因此有初动能和末动能等概念。

说明:A AB为合外力做的功;从广义上说,合外力所做的功在数值上等于物体总能量的改变,功是能量改变的量度;动能是标量,只有正值;A AB只与始末状态的动能改变有关,不管是恒力还是变力,过程如何复杂。

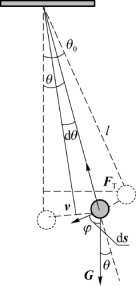
图4.7　例4.1用图

例4.1 如图4.7所示,质量为1.0 kg的小球系在长为1.0 m细绳下端,绳的上端固定在天花板上。起初把绳子放在与竖直线成角θ0处,然后放手使小球沿圆弧下落。试求绳与竖直线成角θ时小球的速率。

解 在合外力作用下,小球在圆弧上有无限小位移d r时,合外力F做的功为

d A=F·d r=F T·d r+G·d r=G·d r

因为

d s=-l dθ

所以

G·d r=-mgl dθcosφ=-mgl sinθdθ

在摆角由θ0改变为θ的过程中,合外力所做的功为