3.5.2 质点系的角动量守恒定律
由质点系的角动量定理知,若对于某点而言,质点系所受的外力矩之和为零,则质点系对该点的角动量不随时间改变,即若M外=0,则
![]()
这是扩展到质点系的角动量守恒定律。
注意:M外=0与F外=0是独立的,故质点系角动量守恒和动量守恒也是相互独立的。角动量守恒定律是继动量守恒定律之后得到的又一重要守恒定律,如果说动量是与平动相联系的一个守恒量的话,角动量则可以认为是与转动相联系的守恒量。
例3.16 如图3.25所示,长为a的轻质细杆可在光滑水平面上绕过中心的竖直轴转动,细杆的两端分别固定质量为m 1和m 2的小球,且静止不动。有一质量为m 3的黏性泥团以水平速度v 0且与杆成θ角的方向射向m 2,并黏在m 2上,设m 1=m 2=m 3,求杆开始旋转时的角速度ω。
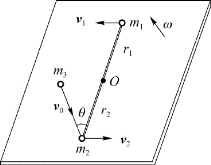
图3.25 例3.16用图
解 将三个质点m 1、m 2和m 3设想为一个质点系,在m 3与m 2碰撞的过程中,作用在轴O上的合外力矩为零。系统对O轴角动量守恒。碰撞前m 1和m 2静止,系统角动量L 0=r 2·m 3v 0 sinθ,碰撞后三个质点都在运动并且有相同的角速度,系统角动量L=r 1·m 1v 1+r 2·m 2v 2+r 3·m 3v 3,角动量守恒,故应用
r 2·m 3v 0 sinθ=r 1·m 1v 1+r 2·m 2v 2+r 3·m 3v 3
由于
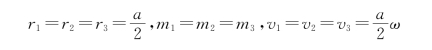
可以解出
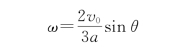
值得注意的是,在m 3与m 2碰撞的过程中,由于轴O上存在着冲力(外力),系统的动量不守恒,但对O轴的合外力矩为零,故对O轴的角动量是守恒量。
阅读材料
火箭飞行原理
在火箭发射过程中,燃料不断燃烧变成热气体,并以高速从火箭尾部向后喷出,因而推动火箭向前作加速运动。
设火箭在外层空间飞行,在t 0时刻的速度为v 0,火箭(包括燃料)的总质量为M 0,热气体相对火箭的喷射速度为u。
随着燃料的消耗,火箭质量不断减少,火箭速度不断加快,燃料用尽后的火箭质量为M,此时火箭所获得的速度v是多少呢?下面具体计算。
第一步:讨论在任意时刻火箭的飞行情况,选取某一时刻t的火箭(包括火箭体和其中尚存的燃料)作为研究的系统,分析此系统的运动情况。设某一时刻t,火箭的质量为m,相对地面的速度为v;在t+d t时间内,火箭喷出的质量为d m(d m是质量m在d t时间内所喷出的质量)的气体。喷出的气体相对火箭的速度为u,方向与v相反。
选择火箭和喷气所组成的部分为系统。
·喷气前:总动量为mv。
·喷气后:火箭动量为(m-d m)(v+d v);喷出的气体的动量为d m(v+d v-u)。
忽略空气阻力和重力,系统动量守恒。
第二步:应用动量守恒定律,有
mv=(m-d m)(v+d v)+d m(v+d v-u)
忽略高阶无穷小,并整理后得m d v+u d m=0,即
![]()
对上式两边积分,从t 0到t时刻的时间内,其速度变化为v 0→v,其质量由M 0变化为M,于是有
所以
即
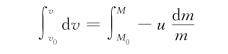
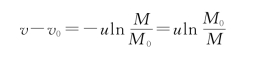
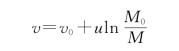
这就是从t 0时刻到t时刻,火箭的质量从M 0变为M时火箭的速度公式。
第三步:求火箭在全部燃料用完时的速度。
如果设火箭开始飞行时速度为零(v 0=0),燃料用尽时质量为M,那么根据上式解得火箭能够达到的速度为
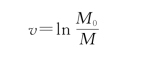
其中,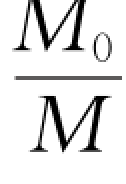 称为火箭的质量比。
称为火箭的质量比。
要把航天器发射上天,则火箭获得的速度至少要大于第一宇宙速度。若要使航天器离开地球到达其他行星或脱离太阳系到其他星系,则火箭获得的速度应分别大于第二宇宙速度和第三宇宙速度。但是按计算可得一级火箭的速度是v f≈10.8 km/s,由于此式导出时未计入地球引力和空气摩擦力产生的影响,加上各种技术的原因,单级火箭的末速度v f将小于第一宇宙速度v 1=7.9 km/s。这就是说,单级火箭并不能把航天器送上天。运载火箭通常为多级火箭,多级火箭是用多个单级火箭串联、并联或串并联组合而成的一个飞行整体。
![]()
1.冲量
(1)恒力的冲量
对于恒力,有
I=F(t 2-t 1)=FΔt
(2)变力的冲量
元冲量为
d I=F d t(https://www.daowen.com)
一般来说,质点在合力F作用下沿曲线运动,则在t 1到t 2的作用时间内变力F的冲量为
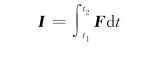
2.动量定理
(1)质点的动量定理
微分形式为
F d t=d p
或
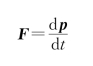
积分形式为
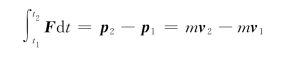
(2)质点系的动量定理
微分形式为
F外d t=d p
或
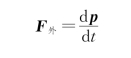
其中,![]() ,F外为质点系所受外力的合力。
,F外为质点系所受外力的合力。
积分形式为
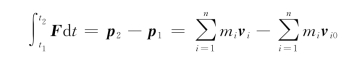
3.动量守恒定律
当系统所受合外力为零时,即F外=0时,系统的总动量保持不变,即
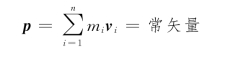
4.质心、质心运动定律
质心的位置矢量为
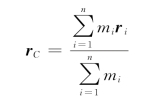
在直角坐标系中
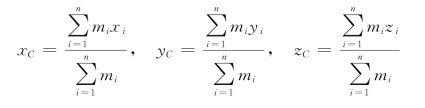
或
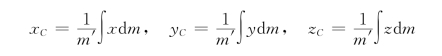
质心运动定律为
F=m a C
5.角动量
力矩为
M=r×F
力对参考点的力矩大小为
M=rF sinθ
(1)单个质点
质点的角动量为
L=r×p=r×m v
质点的角动量定理为
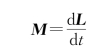
质点所受的合外力矩等于它的角动量对时间的变化率。
质点的角动量守恒定律:若质点所受的合力矩为零,即M=0,则质点的角动量保持不变。
(2)质点系
质点系的角动量定理为

质点系的角动量守恒定律:若质点系所受的外力矩之和为零,则质点系对该点的角动量不随时间改变,即若M外=0,则

