4.4.3 能量守恒定律
在长期的生产实践和科学实验中,人们总结出一条重要的结论:对于孤立的系统来说,系统内各种形式的能量是可以相互转换的,但是不论如何转换,能量既不能产生,也不能消失。这一结论叫作能量守恒定律,它是自然界中的普遍规律。能量守恒不仅适用于物体的机械运动、热运动、电磁运动、核子运动等物理运动形式,而且也适用于化学运动、生物运动等运动形式。它体现了运动的守恒。应当指出,在能量转换的过程中,能量的变化常用功来量度。在机械运动范围内,功是机械能变化的唯一量度。但是,不能把功与能量等同起来,因为功是和能量转换过程联系在一起的,而能量则只和系统的状态有关,是系统状态的函数。
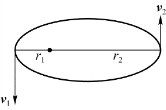
图4.12 例4.3用图
例4.3 行星在椭圆轨道上绕太阳运动,如图4.12所示,太阳质量为m 1,行星质量为m 2,行星在近日点和远日点时离太阳中心的距离分别为r 1和r 2,求行星在轨道上运动时的总能量。
解 将行星与太阳视为一个系统,由于只有引力做功,系统机械能守恒。设行星在近日点和远日点时的速率分别为v 1和v 2,有
![]()
行星在轨道上运动时,受太阳的万有引力作用,引力的方向始终指向太阳,以太阳为参考点,行星所受力矩为零,故行星对太阳的角动量守恒,即
m 2r 1v 1=m 2r 2v 2
行星在轨道上运动时的总能量
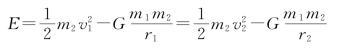
联立以上三式解得
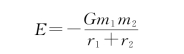
例4.4 如图4.13所示,雪橇从高50 m的山顶A点沿冰道由静止下滑,坡道AB长500 m,滑至B点后,又沿水平冰道继续滑行若干米后停止在C点处。若μ=0.050,求雪橇沿水平冰道滑行的路程。
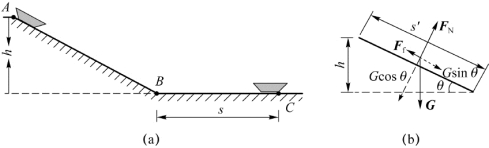
图4.13 例4.4用图
解 已知h=50 m,μ=0.050,s′=500 m,
W f=-μmg cosθs′-μmgs≈-μmg(s′+s)
E 2-E 1=-mgh
整个滑行过程摩擦力做的功为
A f=-μmg cosθs′-μmgs≈-μmg(s′+s)
系统机械能的变化为
E 2-E 1=-mgh
根据功能原理A f=E 2-E 1,解得
![]()
例4.5 如图4.14所示,一轻弹簧一端系在铅直放置的圆环的顶点P,另一端系一质量为m的小球,小球穿过圆环并在环上运动(μ=0)。开始时球静止于A点,弹簧处于自然状态,其长为环半径R,当球运动到环的底端B点时,球对环没有压力。求弹簧的劲度系数。
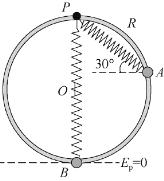
图4.14 例4.5用图
解 以弹簧、小球和地球为一个系统。根据已知条件推出,弹簧的原长为R。
因为从A到B只有重力和弹簧弹力这两个保守内力做功,所以系统E B=E A。
取点B为重力势能零点,在B点弹簧的伸长量为R,有
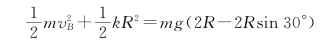
又在最低点B点,弹力和重力的合力提供了向心力,即
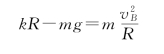
所以
![]()
例4.6 如图4.15所示,在光滑的水平桌面上A点处放有质量为m 0的木块,木块与弹簧相连,弹簧的另一端固定在O点,其劲度系数为k。开始时弹簧处于自由长度l 0。设有一质量为m的子弹以速度v 0沿垂直于OA方向射入木块,并嵌在其中。当木块运动到B点时,弹簧长度为l,试求木块在B点时的速度v的大小和方向。
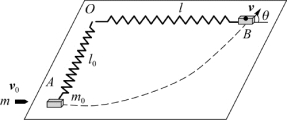
图4.15 例4.6用图
解 本题可分为两个过程:子弹射入木块以及子弹和木块一起从A点运动到B点。
在第一个过程中,子弹和木块的总动量守恒,取子弹初速度方向为正,有
mv 0=(m+m 0)v 1
在第二个过程中,子弹、木块和弹簧的机械能和角动量守恒,取O点为参考点,弹簧原长为零势能点,有
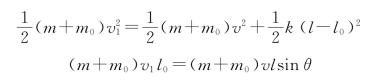
解得
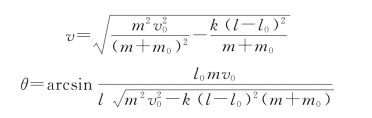 (https://www.daowen.com)
(https://www.daowen.com)
![]()
1.功
恒力的功为
A=F·Δr
元功为
d A=F·d r=F cosθd r
变力的功:质点从A到B外力所做的功为
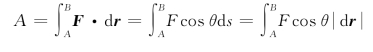
在直角坐标系中,
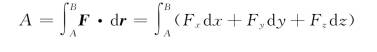
2.动能定理
质点的动能定理为

质点系的动能定理为
A外+A内=E k2-E k1
3.保守力和势能
(1)保守力
做功只与始、末位置有关,与经过的路径无关的力。
物体沿任意闭合路径运动一周时,保守力对它做功为零,即
![]()
(2)势能
势能的定义为
Aab=E p a-E p b=-(E p b-E p a)=-ΔE p
势能的计算公式为
![]()
上式是势能计算的普遍公式,根据这个公式,空间某点(某位形)的势能等于保守力由该点(r)到势能零点(r 0)所做的功。
(3)几种势能及零势能点
·重力势能为
E p=mgh(h=0处为势能零点)
·弹簧的弹性势能为
![]()
·万有引力势能为
![]()
4.质点系的功能原理和机械能守恒定律
质点系的功能原理为
![]()
即
![]()
![]()
机械能守恒定律:当A ex+A innc=0时,有
E=E 0
即
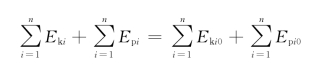
或
ΔE k=-ΔE p
