9.2.3 劈尖和牛顿环
前面我们讨论的是平行光束入射到厚度均匀的薄膜上的干涉情况。在厚度不均匀的薄膜上所产生的干涉现象也是常见的,在这里我们介绍劈尖和牛顿环。
1.劈尖
如图9.17(a)所示,两块平面玻璃片,一端相互叠合,另一端垫入一薄物或细丝,这样在两玻璃片之间形成一空气层,称之为空气劈尖。两玻璃片的交线称为棱边,在与棱边平行的线上,空气劈尖的厚度是相等的。图9.17中M为半透明反射镜,L为透镜,T为显微镜,S为置于L焦点上的单色点光源。由S发出的光经L后成为平行单色光垂直照射于劈头上,即i=0,此时由空气膜上、下两表面反射回来的光构成相干光,可观察到明暗相间、均匀分布的干涉条纹,如图9.17(c)所示。这种干涉即称为劈尖干涉。
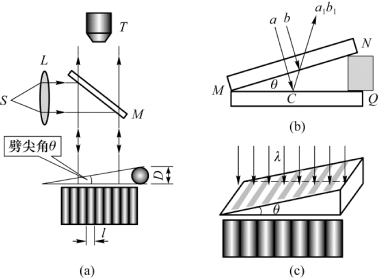
图9.17 劈尖干涉
如图9.17(b)所示,劈尖C点处厚度为e,当波长为λ的平行单色光垂直(i=0)入射时,在劈尖上下两表面反射的两条相干光线间的光程差为
![]()
其中,n为空气折射率,λ/2是由于光线a a 1在劈尖下表面反射时具有半波损失而附加的。因此,反射光的干涉条件为
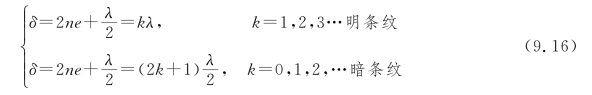
由式(9.16)可见,对应于劈尖厚度相同的地方,两相干光的光程差都一样,对应于同一级干涉条纹,称这种与膜一定厚度相对应的干涉条纹为等厚干涉条纹,这种干涉又称为等厚干涉。因此,劈尖的干涉条纹应是一系列平行于劈尖棱边的明暗相间的等间距直条纹。
在两玻璃片相接触的棱边处,劈尖厚度e=0,由于存在半波损失,因而光程差δ=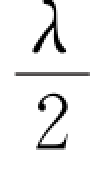 ,所以棱边处应为暗条纹,这与实际观察到的现象是相符的,反过来也证明了半波损失的确是存在的。如图9.17(c)所示,两相邻明条纹或暗条纹的间距以l表示,则有
,所以棱边处应为暗条纹,这与实际观察到的现象是相符的,反过来也证明了半波损失的确是存在的。如图9.17(c)所示,两相邻明条纹或暗条纹的间距以l表示,则有
![]()
根据式(9.14)的暗纹条件有
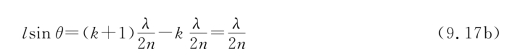
显然两相邻暗条纹间距与两相邻明条纹间距相等。式(9.17)中θ为劈尖夹角。显然θ越小,干涉条纹越疏;θ越大,干涉条纹越密。若劈尖的夹角θ很大,则干涉条纹将密得无法分开,也就无法观察了。一般来说,劈尖干涉条纹只能在劈尖夹角很小的情况下观察到。
在实际工作中可应用劈尖干涉的原理检测工件表面的平整情况,设图9.17(b)中的MQ为被检测的工件表面,MN为一光学平面的标准玻璃片。如果被检测工件表面MQ也是光学平面,则干涉条纹为间距相等的平行直条纹。如果MQ的表面稍有凹凸情形,则在相应处的干涉条纹将发生畸变,不再是平行直条纹,而是疏密不均的曲线形条纹。
应用劈尖干涉的原理还可以测量微小线度。根据式(9.17b),若已知入射单色光波长λ和劈尖折射率n,又可测出条纹间距l,则可求得劈尖夹角θ,这样就可进一步求出两块玻璃片所夹薄物的线度。若夹的是一细金属丝,则可求得金属丝的直径。
应用劈尖干涉的原理还可测量微小的线度变化。例如,图9.17(c)中空气劈尖的夹角θ不变,只改变NQ,亦即在保持玻璃片MN不动的情况下使玻璃片MQ向上平移,则由式(9.16)可知,等厚干涉条纹将发生级次移动。设空气折射率n≈1,若NQ的厚度变化λ/2,即MQ向上平移λ/2距离,则原来的第k级干涉暗纹将移到原来的第k+1级暗纹位置处,第k+1级移到第k+2级位置处,依此类推,整个干涉条纹图样将沿劈尖的上表面MN向较厚的方向移动一个条纹间距l。如果NQ的厚度减少了m个λ/2,则整个条纹图样移动ml距离,于是通过测量条纹移动的距离ml,或数出越过视场中某一刻度线的明条纹或暗条纹的数目m,即可由公式Δe=ml sinθ=m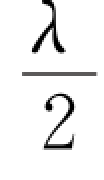 ,求得NQ尺度的微小变化,利用这个原理制成的干涉膨胀仪可测量很小的固体样品的线膨胀系数。
,求得NQ尺度的微小变化,利用这个原理制成的干涉膨胀仪可测量很小的固体样品的线膨胀系数。
例9.5 利用劈尖干涉检验精密加工工件表面的质量。在工件上放一光学玻璃,一端垫起,使其间形成一空气劈尖,如图9.18(a)所示。今观察到干涉条纹如图9.18(b)所示。试根据条纹弯曲方向,判断工件表面是凹还是凸。
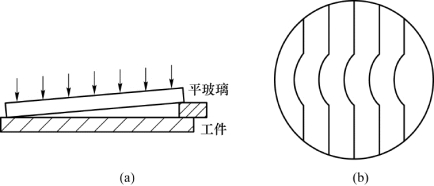
图9.18 例9.5用图
解 由于光学平面玻璃的表面是很平的,所以若工件表面也是平的,则空气劈尖的等厚干涉条纹应为平行于棱边的直条纹。现在干涉条纹的局部弯向棱边,说明在工件表面的相应位置处有一条垂直于棱边的不平的纹路。根据式(9.16),我们知道,同一条等厚干涉条纹对应的薄膜厚度相等,所以在同一条纹上,弯向棱边的部分和直的部分所对应的膜厚度应该相等,本来越靠近棱边的膜厚度应越小,而现在在同一条纹上近棱边处和远离棱边处厚度相等,这说明工件表面的纹路是下凹的。
例9.6 用波长λ=589.0 nm的激光垂直照射一折射率n=1.52的玻璃劈尖,在玻璃表面上产生等厚干涉条纹。今测得两相邻暗条纹间距l=0.25×10-2 m,试求此劈尖的夹角θ。
解 由于钠光垂直照射玻璃劈尖,则
![]()
故(https://www.daowen.com)
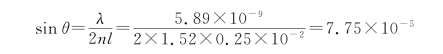
因为θ角很小,所以sinθ≈θ,则
θ=9.683×10-5 rad
2.牛顿环
将一曲率半径很大的平凸透镜A的凸面放在一片光学平玻璃B的上面,如图9.19所示。在凸面与平面之间形成了一空气薄层。
从接触点O向外,空气薄层的厚度逐渐增大,并且在以接触点O为中心的任意一圆上的各点处,空气薄层的厚度都相等。设有一单色平行光束经45°倾角的半透明的平面镜M反射后,垂直照射到平凸透镜的表面上,则在空气薄层的上下两个界面(透镜的凸面和平面玻璃片的上表面)上反射的两条光线为相干光线,将发生干涉,于是通过透镜可以观察到在透镜的凸面和空气薄层的交界面上产生以接触点O为中心的明暗相间的环形干涉条纹,如图9.19(b)所示,随着环半径的增大,明暗环变得越来越密。由于每一环干涉条纹所在处的空气薄层的厚度相等,所以这些干涉条纹也是一种等厚干涉条纹,称这样的干涉条纹为牛顿环。
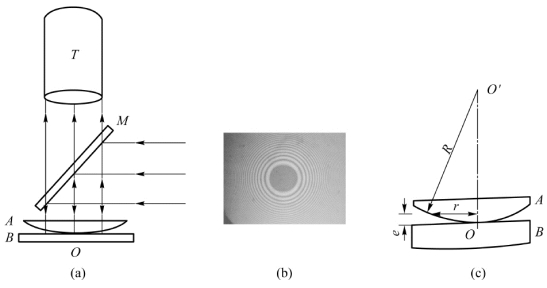
图9.19 牛顿环实验
现在来定量地计算牛顿环的半径r、光波波长λ和平凸透镜的曲率半径R之间的关系。由于透镜及玻璃片的折射率都比空气的折射率n大,则对应空气薄膜任一厚度e处,两束相干光的光程差为
![]()
式(9.18)中,λ/2是光在空气薄膜的下表面(即与平面玻璃片的分界面)上反射时产生的半波损失,则产生明、暗环的条件为
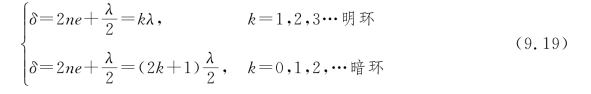
设平凸透镜的曲率半径为R,某一级牛顿环的半径为r,从图9.19(c)中的直角三角形可得空气薄膜任意一点处膜厚e与R和r的关系为
r 2=R 2-(R-e)2=2Re-e 2
因为R≫e,故可以略去上式中的e 2,于是得
r 2=2Re
由式(9.18)中解出e,代入上式可求得明环和暗环的半径分别为

在平凸透镜的凸面与玻璃片的接触点O处,因为e=0,由式(9.18)可知,两条反射光线的光程差δ=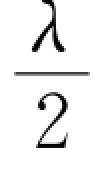 ,所以牛顿环的中心点是一暗点(实际上是一个暗圆面,因为接触点实际上不是点而是圆面)。
,所以牛顿环的中心点是一暗点(实际上是一个暗圆面,因为接触点实际上不是点而是圆面)。
可以看出,当第k级明环或暗环半径r k测得后,若已知入射光的波长λ,则可算得平凸透镜的曲率半径R;反之,若R为已知,则可算得入射光的波长λ。
牛顿环干涉图样中任何两相邻明环或相邻暗环间的半径之差rk+1-rk与环半径之间的关系可由式(9.20)导出,即
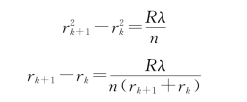
从上式可以看出,k越大,环的半径越大,但相邻两明环或暗环的半径之差越小,这表明随着环半径逐步增大,牛顿环变得越来越密,这正如图9.19(b)所显示的一样。
如果用白光照射到平凸透镜的表面上,由式(9.20)可以看出,不同波长的光对应同一级次k产生的明环半径r k不同,干涉条纹是彩色的环谱。
以上讨论了反射光的干涉问题,透射光也可以产生牛顿环,只是其明暗情形与反射光的明暗情形恰好相反,透射光干涉产生的牛顿环中心处是一亮圆面。
除了可以用牛顿环测量平凸透镜的曲率半径及未知入射单色光的波长外,在制作光学元件时,常常根据牛顿环环形干涉条纹的圆形程度来检验平面玻璃是否为光学平面或透镜的曲率半径是否均匀。前者是把标准的平凸透镜放在受检的玻璃片上进行检验,后者是把磨好的平凸透镜放在标准的光学平面玻璃片上进行检验。另外,也可以应用牛顿环法检验平凸透镜曲率半径的大小是否合格,方法是用曲率半径为标准值的凹面玻璃与一受检验的平凸透镜叠在一起,如果两者完全密合,则不出现牛顿环;如果平凸透镜的曲率半径稍偏离标准值,则产生牛顿环。
