7.1.2 毕奥-萨伐尔定律的应用
例7.1 如图7.3所示,设有一段直载流导线,电流强度为I,P点距导线为a,求P点的B。
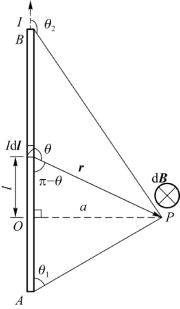
图7.3 例7.1用图
解 在AB上距O点为l处取电流元I d l,I d l在P点产生的d B的大小为
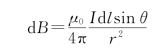
d B方向垂直指向纸面(I d l×r方向)。同样可知,AB上所有电流元在P点产生的d B方向均相同,所以P点B的大小即等于下面的代数积分
![]()
统一变量,由图7.3知,

可知
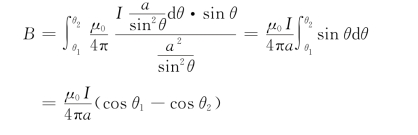
B垂直指向纸面。
如果载流导线是一无限长的直导线,那么可以认为θ1=0,θ2=π,所以
![]()
例7.2 如图7.4所示,在一半径为R的圆形载流导线中通过的电流为I,求在垂直于圆面并通过圆心的轴线上任意点P的磁感应强度。
解 建立坐标系Oxy,任取电流元I d l,I d l在P点产生的磁感应强度为d B,大小为d B=![]() 。
。
d B的方向垂直于电流元I d l和矢径r所组成的平面,由于圆形导线上各电流元在P点所产生的磁感强度的方向不同,因此把d B分解成两个分量:平行于x轴的分量d B∥和垂直于
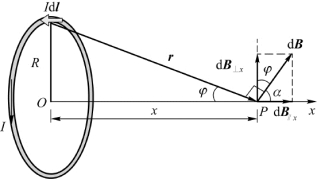
图7.4 例7.2用图(圆电流的磁场)
x轴的分量d B⊥。在圆形导线上,由于同一直径两端的两电流元在P点产生的磁感应强度对x轴是对称的,所以它们的垂直分量d B⊥互相抵消,于是整个圆形电流的所有电流元在P点产生的磁感应强度的垂直分量d B⊥两两相抵,所以叠加的结果是只有平行于x轴的分量d B∥,即有(https://www.daowen.com)
合磁场的磁感应强度为
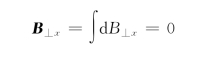
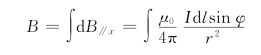
r 2=x 2+R 2,sinφ=R/x 2+R 2,与d l无关。
圆电流在P点的总磁场大小为
![]()
B的方向沿轴线与线圈中电流的方向成右手螺旋关系,即用右手四指表示电流的流向,大拇指所指的方向就是磁场的方向。
在线圈中心处的O点,x=0,有
![]()
如果载流线圈是由紧靠在一起、载流为I的N匝相同圆线圈组成的,那么轴线上某点处的磁感应强度大小为

运用毕奥-萨伐尔定律解题的步骤如下:
(1)建立适当的坐标系;
(2)选取合适的电流元;
(3)写出d B,并写出各分量d B x、d By、d Bz;
(4)分别积分,![]() ,求出B(大小和方向)。
,求出B(大小和方向)。
引入磁矩来描述载流线圈的性质。载流线圈的面积为S,电流为I,电流流向与线圈平面的法向单位矢量e n满足右手螺旋法则,则磁矩可定义为
m=IS e n
N匝密绕相同线圈的磁矩为
m=NIS e n
