习 题
一、选择题
1.一质点在平面上运动,已知质点位置矢量的表示式为r=at 2i+bt 2j(其中a、b为常量),则该质点做( )。
A.匀速直线运动 B.变速直线运动
C.抛物线运动 D.一般曲线运动
2.一质点在平面上做一般曲线运动,其瞬时速度为v,瞬时速率为v,某一段时间内的平均速度为v,平均速率为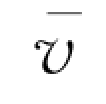
,它们之间的关系必定有( )。
3.质点做半径为R的变速圆周运动时的加速度大小为(v表示某一时刻质点的速率)( )。
4.某物体的运动规律为d v/d t=-kv 2,式中的k为大于零的常数。当t=0时,初速度为v 0,则速度v与时间t的函数关系是( )。
5.某人骑自行车以速率v向正东方行驶,遇到由北向南刮的风(设风速大小也为v),则他感到风是从( )。
A.东北方向吹来 B.东南方向吹来
C.西北方向吹来 D.西南方向吹来
6.一飞机相对空气的速度大小为200 km/h,风速为56 km/h,方向从西向东,地面雷达测得飞机的速度大小为192 km/h,方向是( )。
A.南偏西16.3° B.北偏东16.3°
C.向正南或向正北 D.西偏北16.3°
E.东偏南16.3°
7.一小球沿斜面向上运动,其运动方程为s=5+4t-t 2(SI),则小球运动到最高点的时刻应是( )。
A.t=4 s B.t=2 s C.t=8 s D.t=5 s
8.在相对地面静止的坐标系内,A、B两船都以2 m/s的速率匀速行驶,A船沿x轴正向,B船沿y轴正向。今在A船上设置与静止坐标系方向相同的坐标系(x、y方向单位矢量用i、j表示),那么在A船上的坐标系中,B船的速度(以m/s为单位)为( )。
A.2i+2j B.-2i+2j C.-2i-2j D.2i-2j
二、填空题
1.一物体悬挂在弹簧上,在竖直方向上振动,其振动方程为y=A sin wt,其中A、w均为常量,则
(1)物体的速度与时间的函数关系式为________;
(2)物体的速度与坐标的函数关系式为_________。
2.灯距地面高度为h 1,一个人身高为h 2,在灯下以匀速率v沿水平直线行走,如习题图1.1所示。则他的头顶在地上的影子M点沿地面移动的速度v M=_________。
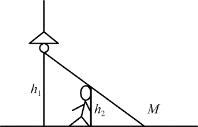
习题图1.1
3.试说明质点做何种运动时,将出现下述各种情况(v≠0):
(1)a t≠0,a n≠0_________________
(2)a t≠0,a n=0________________
a t、a n分别表示切向加速度和法向加速度的大小。
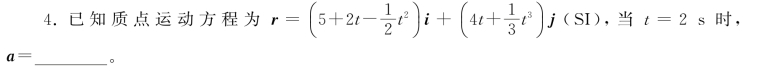
5.一质点以60°仰角做斜上抛运动,忽略空气阻力。若质点运动轨道最高点处的曲率半径为10 m,则抛出时初速度的大小为v 0=________。(重力加速度g按10 m/s2计)
6.质点沿半径为R的圆周运动,运动学方程为θ=3+2t 2(SI),则t时刻质点的法向加速度大小为a n=________________;角加速度β=________________。
7.一物体做如习题图1.2所示的斜抛运动,测得在轨道A点处速度v的大小为v,其方向与水平方向夹角成30°。则物体在A点的切向加速度a t=________,轨道的曲率半径ρ=_________。
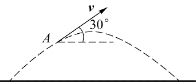
习题图1.2
8.有一水平飞行的飞机,速度为v 0,在飞机上以水平速度v向前发射一发炮弹,略去空气阻力,并设发炮过程不影响飞机的速度,则
(1)以地球为参照系,炮弹的轨迹方程为________。
(2)以飞机为参照系,炮弹的轨迹方程为________。
三、计算题
1.一质点沿x轴运动,其加速度a与位置坐标x的关系为a=4x+2(SI)。如果质点在原点处的速度为v 0=2 m/s,试求其在任意位置处的速度。
2.一质点沿直线运动,其运动学方程为x=6t-t 2(SI)。求:
(1)在t从0～4 s的时间间隔内,质点的位移大小;
(2)在t从0～4 s的时间间隔内质点走过的路程。
3.质点在x Oy平面上运动,运动学方程为r=a cosωt i+b sinωt j,式中a、b、ω为正的常量。试求:
(1)质点运动的轨道方程;
(2)质点的速度和加速度;
(3)证明加速度方向指向坐标原点。
4.一质点沿半径为R的圆周运动,质点所经过的弧长s与时间t的关系为s=bt+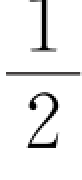
ct 2,其中b、c是大于零的常量,求从t=0开始到达切向加速度与法向加速度大小相等时所经历的时间。
5.一人站在山脚下向山坡上扔石子,石子初速度为v 0,与水平夹角为θ(斜向上),山坡与水平面成α角。
(1)如果不计空气阻力,求石子在山坡上的落地点与山脚的距离s;
(2)如果α与v 0一定,θ取何值时s最大,并求出最大值s max。
6.质点P在水平面内沿一半径为R=2 m的圆轨道转动。转动的角速度ω与时间t的函数关系为ω=kt 2(k为常量)。已知t=2 s时,质点P的速度大小为32 m/s。试求t=1 s时,质点P速度与加速度的大小。
7.一飞机驾驶员想往正北方向航行,而风以60 km/h的速度由东向西刮来,如果飞机的航速(在静止空气中的速率)为180 km/h,试问:
(1)驾驶员应取什么方向航行?
(2)飞机相对于地面的速率为多少?试用矢量图说明。
8.已知质点位矢随时间变化的函数形式为r=t 2i+2t j,式中r的单位为m,t的单位为s。求:
(1)任一时刻的速度和加速度;
(2)任一时刻的切向加速度和法向加速度。