7.1.1 电流元电流元的磁场
导体中不随时间变化的电流叫作恒定电流(也叫作直流电)。恒定电流的磁场分布不随时间而变化,这样的磁场称为恒定磁场或静磁场。
在静电场中我们曾经讲过,求带电体场强时,把带电体看成由许多电荷元组成,写出电荷元的场强表达式之后,然后用叠加法求整个带电体的场强。将这一微元法应用到求载流导线的磁感应强度中,把载流导线看作由许多电流元组成的,如果已知电流元产生的磁感应强度,用叠加法(实验表明叠加法成立),便可求出整个线电流的磁感应强度。电流元的磁感应强度由毕奥-萨伐尔定律给出(这条定律是毕奥、萨伐尔等人对实验资料加以分析和总结得出的,故称毕奥-萨伐尔定律)。
假设真空中有任意形状的导线,如图7.2所示,通有稳恒电流I,在导线上沿电流方向取d l,这个线元很短,可看作直线段,则I d l称为电流元。为了求得任意形状的载流导线所产生的磁场,我们可以将载流导线分割成许多电流元I d l。
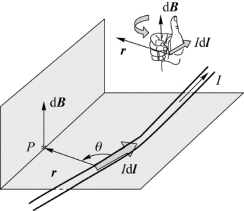
图7.2 电流元的磁场
电流元I d l在空间任意一点P产生的磁感应强度d B遵守毕奥-萨伐尔定律:d B的大小与电流元I d l的大小成正比,与电流元和由电流元到点P的矢量r之间夹角的正弦成正比,与电流元到点P的距离的平方成反比;d B的方向垂直于I d l和r所组成的平面,其指向满足右手定则。用数学式子可以表示为其中,μ0称为真空磁导率,μ0=4π×10-7 N/A 2;e r是r方向的单位矢量。
 (https://www.daowen.com)
(https://www.daowen.com)
d
B的大小为![]() ,d B的方向垂直于电流I d l与r组成的平面。毕奥-萨伐尔定律虽然不能由实验直接验证,但由这一定律出发而得出的一些结果都很好地和实验相符合。
,d B的方向垂直于电流I d l与r组成的平面。毕奥-萨伐尔定律虽然不能由实验直接验证,但由这一定律出发而得出的一些结果都很好地和实验相符合。
要确定任意载有稳恒电流的导线在某点的磁感应强度,根据磁场满足叠加原理,对整个载流导线积分,即得
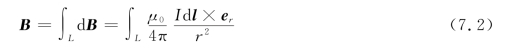
值得注意的是,式(7.2)中每一电流元在给定点产生的d B方向一般不相同,所以式(7.2)是矢量积分式。由于一般定积分的含义是代数和,所以求式(7.2)的积分时,应先分析各电流元在给定点所产生的d B的方向是否沿同一直线,如果是沿同一直线,则式(7.2)的矢量积分转化为

