3.2.1 质点系的动量定理
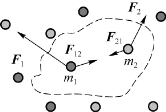
图3.5 质点系动量定理
在一个问题中,如果我们考虑的对象包括几个物体,则它们整体上常被称为一个物体系统,简称为系统。系统外的其他物体统称为外界。系统内各物体间的相互作用力称为内力,外界物体对系统内任意物体的作用力称为外力。例如,把桌子和桌子上放置的物体看成一个系统,则它们之间相互挤压的力称为内力,系统以外的力(如重力)都是外力。下面讨论一个系统的动量变化规律。
先讨论一个简单的系统,如图3.5所示,对于由两个质点组成的质点系,设它们的质量分别为m 1、m 2。它们分别受外力F 1和F 2,内力分别为F 12和F 21,由质点1、2的动量定理有
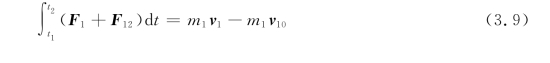
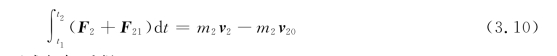
因内力F 12+F 21=0,故将两式相加后得
![]()
推广到n个质点,则有
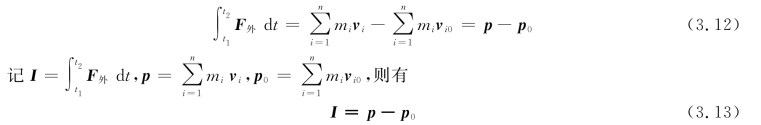
式(3.13)表明,作用于系统的合外力的冲量等于系统动量的增量。这就是质点系的动量定理。
在无限小的时间间隔内,质点系的动量定理的微分形式可写成
![]()
或
 (https://www.daowen.com)
(https://www.daowen.com)
式(3.14)中,p=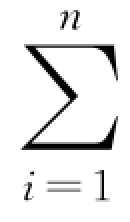 mi v i,F外为质点系所受外力的合力。式(3.15)表明,作用于质点系的合外力等于质点系的动量随时间的变化率。
mi v i,F外为质点系所受外力的合力。式(3.15)表明,作用于质点系的合外力等于质点系的动量随时间的变化率。
动量定理与牛顿定律的关系为:对于一个质点,牛顿定律表示的是力的瞬时效应,而动量定理表示的是力对时间的积累效果;牛顿定律只适用于质点,不能直接用于质点系,而动量定理可用于质点系。
例3.4 长为l、线密度为λ的绳子堆在地上,如图3.6所示,若用手握一端以v匀速向上提,求当端点距地面为x时,提力的大小。
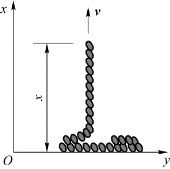
图3.6 例3.4用图
解 解法一:以提起部分为研究对象,因为绳子是柔软的,地面上的绳子对提起部分的绳子既无拉力又无支持力。故提起部分只受拉力F和自身重力的作用。设d x提起时间为d t,根据动量定理有
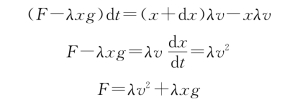
解法二:若选全部绳子为研究对象,地面上的绳子与支持力平衡,故外力只有F-λxg。而
p=λvx
所以
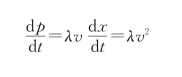
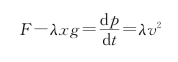
即
F=λv 2+λxg
