2.2.1 万有引力
世界上任何物体之间都存在着一种相互吸引的力,这种力叫作万有引力。牛顿将万有引力遵循的规律总结为万有引力定律:任何两个质点都相互吸引,引力的大小与它们的质量的乘积成正比,与它们的距离的平方成反比,力的方向沿两质点的连线方向。设有两个质量分别为m 1、m 2的质点,相对位置矢量为r,则两者之间的万有引力F为
![]()
式中,e r为r方向的单位矢量。负号表示F与r方向相反,表现为引力。G为引力常量,G=6.67×10-11 N·m2/kg2,其物理意义是:G在数值上等于质量均为1 kg的两个质点相距1 m时相互作用的万有引力。这个引力常量的出现要比万有引力定律晚100多年,是英国的物理学家卡文迪许测出来的。m 1、m 2称为物体的引力质量,是物体具有产生引力和感受引力的属性的量度。
万有引力定律的适用条件为:万有引力定律中的物体是对质点而言的。对于相距很远因而可以看作质点的物体,公式中的r就是指两个质点间的距离;均匀的球体可以看作质量集中于球心上的质点,这是一种等效的简化处理方法。
万有引力定律把地面上的运动与天体运动统一起来,是自然界中最普遍的规律之一。万有引力具有相互性,两物体间相互作用的引力是一对作用力与反作用力。
例2.1 在地球赤道上空距海平面高h处有一人造卫星,可近似看作绕地轴做匀速率圆周运动,其角速率与地球自转角速率相同,即人们看到它在天空不动,称为同步人造卫星。已知同步卫星的周期T=24 h,地球的质量M e=5.98×1024 kg,地球的平均半径R e=6.37×103 km。求它距海平面的高度h。
解 如图2.6所示,卫星的轨道半径为R e+h。因它做匀速率圆周运动,所以只有向心加速度。设卫星的速率为v,则向心加速度为
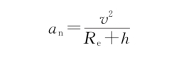
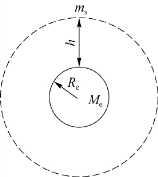
图2.6 例2.1用图
产生向心加速度的原因是受到地球的吸引力。设卫星的质量为m s,根据万有引力定律与牛顿第二定律,有
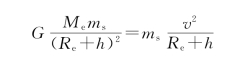
因卫星的轨道周长为2π(R e+h),周期为T,所以其速率为(https://www.daowen.com)
v=2π(R e+h)/T
代入上式可以解出
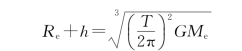
即同步卫星距海平面的高度为
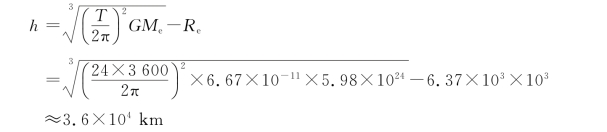
例2.2 已知地球平均半径R e=6.37×103 km,试估算地球的质量及地球的平均密度。
解 由式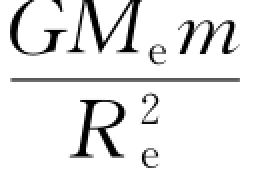 = mg,可得地球的质量为
= mg,可得地球的质量为
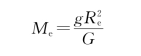
地球表面的重力加速度g可由实验测出,取g=9.81 m/s2,代入上式求出
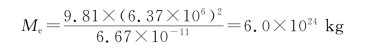
地球的平均密度为
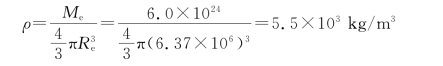
经典力学中常见的力都是来源于自然界基本的相互作用,其细节不在这里讨论。我们在这里讨论的重点是这些宏观特征。
