2.1.4 力的合成与分解
日常生活中常常有这样的情景,一个物体通常会受到几个力的共同作用。例如,两个同学可以共同提起一桶水,也可以让一个同学提这桶水,我们可以说两个同学提水桶的力与一个同学提水桶的力产生的效果是相同的。再如,若一个力产生的效果与原来几个力产生的效果相同,这个力就叫作那几个力的合力,原来的几个力叫作分力。
合力与分力的关系是在“改变运动状态”效果上可以等效替代,只要效果相同,都可以进行代换。等效代替则是物理学中的常用方法。“等效”的基础是在某一方面的“效果相同”,脱离了“效果相同”讲“等效”是毫无意义的。
求几个力的合力的过程叫作力的合成。求一个力的分力的过程叫作力的分解。合力与分力有等效性与可替代性。力的合成与分解遵守平行四边形定则。
实验表明,两个互成角度的共点力的合力,可以用表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向,这就是力的平行四边形定则,如图2.2所示。
注意:在物理学中,求矢量时要注意不仅要求出其大小,还要求出其方向,其方向通常用它与已知矢量的夹角表示。
平行四边形定则是物理学上的重要定则之一,它可由实验总结出来。平行四边形定则对所有的有方向的量(矢量)都是成立的。
根据平行四边形的对边平行且相等,即平行四边形是由两个全等的三角形组成的,平行四边形定则可简化为三角形定则。如图2.3所示,若从O点出发先作出表示力F 1的有向线段OA,再以A点出发作表示力F 2的有向线段AC,连接OC,则有向线段OC即表示合力F的大小和方向。
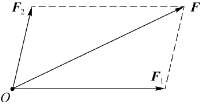
图2.2 平行四边形定则
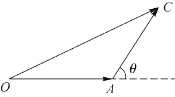
图2.3 三角形定则
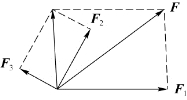
如果几个力都作用在物体的同一点,或者几个力作用在物体上的不同点,但这几个力的作用线延长后相交于同一点,这几个力就叫作共点力。如图2.4所示,求多个力的合成时,可先求任意两个力的合力,再把这个力与第三个力合成,最后得到的平行四边形的对角线即表示合力的大小和方向。
当物体受到多个力的作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便。如果我们将一个力分解为互相垂直的两个力F x和F y,则会使数学计算非常简单,所以解题时常采用这种方式。这种分解方式称为正交分解法,如图2.5所示。
F x=F cosθ, F y=F sinθ
图2.4 共点力的合成
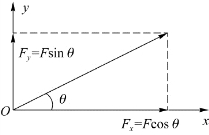
图2.5 力的正交分解
正交分解法的步骤如下。
(1)以力的作用点为原点作直角坐标系,标出x轴和y轴。如果这时物体处于平衡状态,则两轴的方向可根据方便自己选择,一般常使尽可能多的力分布在坐标轴上;若物体有加速度,则通常使一个坐标轴沿加速度的方向。
(2)将各力正交分解在两个互相垂直的坐标轴上。例如,F 1与x轴的夹角为θ1,则F x1=F 1 cosθ1,F y 1=F 1 sinθ1。与两轴重合的力就不需要分解了。然后列出F x、F y的数学表达式:
F x=F x 1+F x 2+F x 3+…, F y=F y1+F y2+F y3+…
(3)求F x和F y的合力的大小,即
,方向(与x轴的夹角)为α=arctan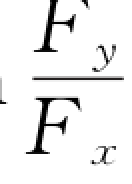
。
合力可能大于任何一个分力,也可能小于任何一个分力,也可能介于两个分力之间。如果两个分力的大小不变,夹角越大,合力就越小;夹角越小,合力就越大。当两个分力F 1、F 2的夹角θ在0°～180°之间变化时,其合力F的变化范围是
|F 1-F 2|≤F≤F 1+F 2
进行力的合成与分解时应注意:合力与分力在效果上是相同的,可以互相替代。在求力的合成时,合力只是分力的效果,实际上并不存在;同样,在求力的分解时,分力只是合力产生的效果,实际上并不存在。因此,在进行受力分析时,不能同时把合力与分力都当作物体所受的力。力的分解虽然有任意性,但在把一个实际的力分解时,一定要看这个力产生的实际效果,而不能任意分解。
力的合成与分解常用到以下两种方法。
(1)作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小。
(2)计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。