2.4.2 力学相对性原理
2026年01月14日
2.4.2 力学相对性原理
设有两个参考系S(Oxyz)和S′(O′x′y′z′),它们的对应坐标轴都相互平行,且Ox轴与Ox′轴相重合,图2.24所示,其中S系是惯性系,S′系以恒定的速度u沿x轴正向相对S系做匀速直线运动,所以S′系也是惯性系。若有一质点P相对S′系的速度为v′,相对S系的速度为v,由1.3节关于速度相对性的讨论可知,它们之间的关系为
v=v′+u
将上式对时间t求导数,并考虑到u为常数,故可得
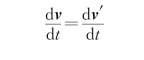
即
![]()
式(2.10)表明,当惯性参考系S′以恒定的速度相对惯性参考系S做匀速直线运动时,质点在这两个惯性系中的加速度是相同的。由于S′系也是惯性系,质点所受的力为F′=m a′。考虑到a′=a,所以(https://www.daowen.com)
F=m a=m a′=F′
这就是说,在这两个惯性性系中,牛顿第二定律的数学表达式具有相同形式,即
F=m a
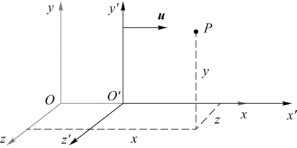
图2.24 力学相对性原理
当由惯性系S变换到惯性系S′时,牛顿运动方程的形式不变。换句话说,在所有惯性系中,牛顿运动定律都是等价的。对于不同的惯性系,牛顿力学的规律都具有相同的形式,在一惯性系内部所作的任何力学实验,都不能确定该惯性系相对于其他惯性系是否在运动。这个原理叫作力学相对性原理或伽利略相对性原理。
