3.4.2 质点的角动量定理力矩
我们引入动量来描述物体的平动状态,它的变化是由力所引起的,二者满足动量定理;对于转动,我们引入角动量来描述物体的运动状态,转动状态也随时间发生变化,这种变化是由谁引起的呢?二者有何规律呢?下面我们来分析质点相对于某一参考点的角动量随时间的变化率与什么因素有关。
一质点在合力F的作用下某瞬间的动量为p=m v,质点相对于参考点O的位置矢量为r,显然此时质点相对于参考点O的角动量为
L=r×p=r×(m v)
两边对时间t求一阶导数,则有
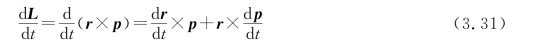
根据速度的定义
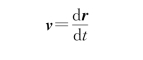
及牛顿第二定律
![]()
可得
![]()
由于速度与动量同向,所以二者的矢量积为零,即
v×p=0
于是得到质点的角动量随时间的变化率的表达式为
![]()
式(3.32)中的r×F引起质点对同一参考点的角动量随时间的变化。
令
M=r×F(https://www.daowen.com)
称为作用于质点的合力F对某参考点O的力矩,如图3.17所示,于是有
![]()
式(3.33)表明,作用于质点的合力对参考点O的力矩等于质点对该点O的角动量随时间的变化率。这与牛顿第二定律F=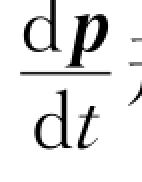 形式上是相似的,只是用M代替了F,用L代替了p。
形式上是相似的,只是用M代替了F,用L代替了p。
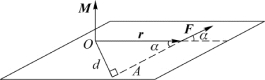
图3.17 力矩的定义
在一般意义上,力矩是对某一参考点而言的。如图3.17所示,力F的作用点相对于参考点O的位矢为r,质量为m的质点在力F的作用下做曲线运动,则F对参考点O的力矩M为
![]()
力矩的大小为M=Fr sinα=Fd,d为力臂,即O到力作用线的垂直距离。力矩是一个矢量。M的方向垂直于r与F所构成的平面,也可由右手定则确定:把右手拇指伸直,其余四指弯曲,弯曲的方向是由径矢r通过小于180°的角α转向力F的方向,这时拇指所指的方向就是力矩的方向。
从力矩的定义可以看出,力矩依赖于参考点O的选择。
作用于质点的合外力矩等于合外力的力矩。

式(3.33)反映了力矩的瞬时作用,现在考虑它对时间的累积效果,即力矩作用在质点上一段时间后对角动量的影响。
将式(3.33)两边同时乘以时间微元d t,得质点角动量定理的微分形式:
![]()
M d t为力矩M与作用时间d t的乘积,叫作冲量矩。
对式(3.36)取积分,得质点角动量定理的积分形式:
![]()
式中,L 1和L 2分别为质点在时刻t 1和t 2对参考点O的角动量,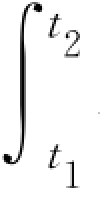 M d t为质点在时间间隔t 1至t 2内对参考点O所受的冲量矩,表示作用于质点上的力矩在这段时间间隔内的时间积累效应。因此,式(3.37)的物理意义是:对同一参考点O,质点所受的冲量矩等于质点角动量的增量。这就是质点的角动量定理。
M d t为质点在时间间隔t 1至t 2内对参考点O所受的冲量矩,表示作用于质点上的力矩在这段时间间隔内的时间积累效应。因此,式(3.37)的物理意义是:对同一参考点O,质点所受的冲量矩等于质点角动量的增量。这就是质点的角动量定理。
