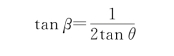1.2.2 抛体运动
1.运动叠加原理和运动的分解
在日常生活和生产实践中,常常可看到一个物体同时参与两个或几个不同方向上运动的情形。大量实验事实表明,宏观物体的一个运动可以看作由几个同时进行且各自独立的运动叠加而成。这称为运动叠加原理或运动独立性原理。
运动叠加原理在日常生活中随处可见。例如,在商场乘坐自动扶梯上行可以看作由水平运动和竖直上升运动叠加而成。
有A、B两小球,在同一时刻、同一高度,使A球做自由落体,B球沿水平方向射出,两球轨迹不同,但总是同时落地。这说明,在同一时间内,A、B两球在竖直方向的位移是相同的,B球的运动可分解为竖直和水平两个方向上的独立运动,即在水平方向做匀速直线运动,在竖直方向做自由落体运动。
一个实际发生的运动可以分解成几个各自独立进行的分运动,这个结论称为运动的分解。
运动的分解是研究曲线运动的一个重要方法。空间中的曲线运动可以分解为三个方向相互正交的直线运动;平面曲线运动可分解为相互垂直方向上的两个直线运动。
一个质点在平面内做曲线运动时,可在运动平面内建立平面直角坐标系x Oy,则质点在t时刻的位置可用坐标(x,y)表示,其矢径、速度、加速度都可用两个分量式表示。质点的运动方程为
![]()
矢量式为
![]()
速度为
![]()
加速度为
![]()
从地面上某点把一物体以某一角度投射出去,物体在空中的运动就叫作抛体运动。如果风力的作用可忽略,则物体的运动轨迹将被限制在通过抛射点的竖直方向与抛出速度方向所确定的平面内,所以是二维运动。这个运动可看作在轨道平面内沿水平方向和竖直方向两个分运动的合成。若不考虑空气阻力的影响,物体只受重力作用,则物体运动的特点是沿水平方向做匀速运动,沿竖直方向以重力加速度g做变速运动。在离地面不太高的范围内,g可看作一常量。
2.平抛运动
平抛运动是指物体只在重力作用下,从水平初速度开始的运动。设有一质点以初速度v 0被水平抛出,做平抛运动。可以将它分解为水平方向以初速度v 0做匀速直线运动,竖直方向做自由落体运动(图1.9)。若以抛出点为原点,x轴沿初速度方向,y轴沿竖直向下方向,建立平面坐标系,则其运动方程为
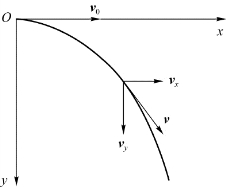
图1.9 平抛运动

或

任一时刻速度为
![]()
请自行求出平抛运动的轨迹方程。
例1.6 如图1.10所示,某人骑摩托车在水平道路上行驶,要在A处越过x=5 m的壕沟,沟面对面比A处低h=1.25 m,摩托车的速度至少要多大(g=10 m/s2)?
解 在竖直方向上,摩托车越过壕沟经历的时间为
![]()
在水平方向上,摩托车能越过壕沟的速度至少为
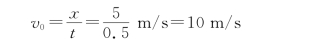
3.斜抛运动
将一物体斜向上(或斜向下)以初速度v 0抛出(图1.11),抛出点为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向。按照正交分解方法,在水平方向质点以初速度v 0 cosθ做匀速直线运动;竖直方向以初速度v 0 sinθ做竖直上抛运动。则物体的两个分运动为
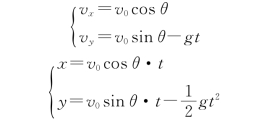
运动学方程为
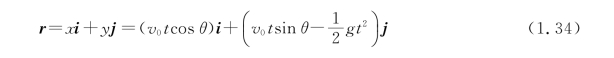
轨迹方程为

图1.10 例1.6图
图1.11 斜抛运动(https://www.daowen.com)
由这两个公式可以导出抛体的射程X(回落到与抛出点高度相同时所经过的水平距离)、射高Y(飞行中的最大高度,即高出抛出点的距离)、飞行时间(回落到抛出点高度所用的时间)T,

在给定初速度的情况下,射程与抛射角有关,当抛射角θ=π/4时,抛体的射程最大,其值为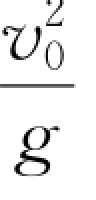 ,如图1.12所示。
,如图1.12所示。
斜抛运动的轨迹是对称的。在上述讨论中,忽略了空气阻力的影响。若空气阻力较大,则抛体的路径为一个不对称的曲线,实际射程比真空射程小,如图1.13所示。
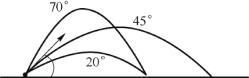
图1.12 射程与抛射角
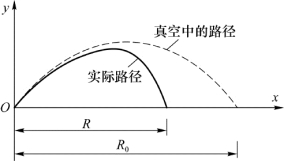
图1.13 空气阻力下的斜抛运动
例1.7 在炮兵射击训练中,通常要求考虑这样的问题:以给定的出口速度v 0(即炮弹在空中飞行的初速度)击中已知距离为X的靶,需要多大的发射仰角α?假定靶和炮在同一水平高度。
解 由射程公式
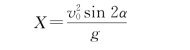
解得

只要X小于最大射程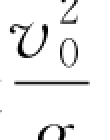 ,α在0~90°有两个解。例如,X=500 m,v 0=100 m/s,则
,α在0~90°有两个解。例如,X=500 m,v 0=100 m/s,则
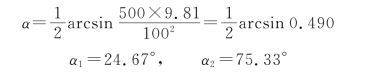
炮弹以这两个仰角发射时,得到相同的射程,都能击中靶心。但以大发射角α2=75.33°发射时,飞行时间长,射高也大。
例1.8 一个人在倾角为θ的斜坡的下端O点处,以与斜坡成β角的初速度v 0抛出一个小球,小球下落时恰好垂直击中斜面。如果不计空气阻力,试证明β满足下列条件:tanβ=![]()
解 取小球为研究对象,视为质点,并使抛出点为坐标原点,沿斜面向上为x轴正方向,垂直于斜面向上为y轴正方向(图1.14)。
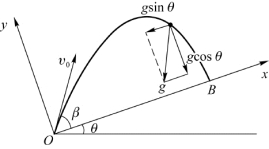
图1.14 例1.8用图
初速度v 0在x、y轴的分量为
v 0x=v 0 cosβ
v 0y=v 0 sinβ
加速度在x、y轴的分量为
a x=-g sinθ
a y=-g cosθ
小球的运动可以分解为x、y方向的匀变速直线运动。其运动方程分别为
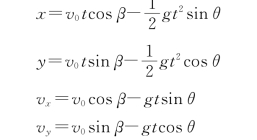
小球下落时恰好垂直击中斜面上的B点,而B点的y坐标为零,即y=0;且小球击中B点时沿x轴方向速度为零,即v x=0。
设击中B点的时间为t B,则有
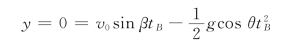
故

将t B代入v x=0,得
0=v 0 cosβ-g sin t B
即
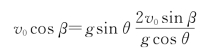
由此即得β应满足的条件为