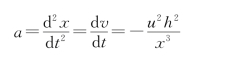1.1.7 加速度
速度是个矢量,它既有大小又有方向。当质点做一般曲线运动时,曲线上各点的切线方向不断改变,所以速度的方向在不断改变;而运动的快慢也可以随时改变,即速度的大小也在不断改变。为了定量地描述各个时刻速度矢量的变化情况,我们引进加速度的概念。
设质点在t时刻位于A点,速度为v A,在t+Δt时刻位于B点,速度为v B,若用Δv表示在时间Δt内质点速度的增量(图1.5),根据矢量运算法则有
![]()
定义Δv与Δt的比值叫作这段时间内的平均加速度,用a表示,即
![]()
平均加速度是矢量,表示质点在确定的时间间隔内速度改变的平均快慢程度,方向就是质点在这段时间内速度增量的方向。在叙述平均加速度时,必须指明在哪一段时间内或哪一段位移上。
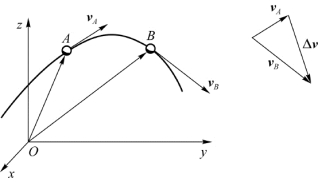
图1.5 速度的增量
和平均速度一样,平均加速度也只是一种粗略的描述,它只代表Δt时间内速度的平均变化率。时间间隔Δt取得越小,则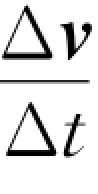 越接近于t时刻速度变化的实际情况。当Δt趋近于零时,平均速度的极限即速度对时间的变化率,叫作质点在时间t的瞬时加速度,简称加速度,用a表示为
越接近于t时刻速度变化的实际情况。当Δt趋近于零时,平均速度的极限即速度对时间的变化率,叫作质点在时间t的瞬时加速度,简称加速度,用a表示为
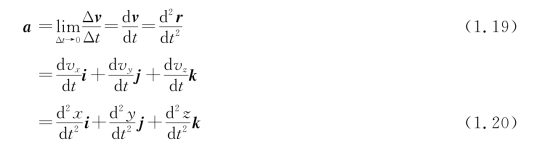
加速度a是速度矢量对时间的一阶导数,其意义为速度矢量随时间的变化率。同时,加速度也是位置矢量对时间的二阶导数。
标量式为

加速度的大小为
![]()
由加速度的三个分量可以确定加速度的方向余弦。
加速度也是一个矢量。加速度的方向就是Δt趋近于零时,平均加速度或速度增量Δv的极限方向,因而加速度的方向与同一时刻速度的方向一般不一致。在直线运动中,加速度的方向与速度方向相同或相反;在曲线运动中,加速度的方向总是指向曲线的凹侧。质点的加速度描述质点速度的大小和方向变化的快慢,由于速度是矢量,所以无论是质点的速度大小还是方向发生变化,都意味着质点有加速度。
在不同的参考系中,同一质点的加速度是不同的。在国际单位制中,加速度的单位是m/s2。
例1.2 一质点在平面上运动,已知质点位置矢量的表达式为r=at 2i+bt 2j(其中a、b为常量),则该质点做何种形式的运动?
解 由质点的位置矢量r=at 2i+bt 2 j得运动方程
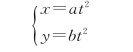
轨道方程
质点的速度
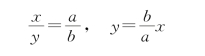
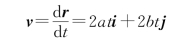
质点的加速度
![]()
质点的加速度为非零恒量,且质点的运动轨迹是直线,故该质点在x Oy平面内做匀变速直线运动,其轨道方程为y=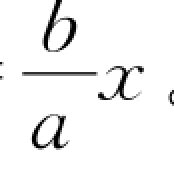 。
。
例1.3 一质点的运动方程为x=4t 2,y=2t+3,其中x和y的单位是米(m),t的单位是秒(s)。试求:
(1)运动轨迹;
(2)第1 s内的位移;
(3)t=0 s和t=1 s两时刻质点的速度和加速度;
(4)t=0 s到t=2 s内的平均速度。(https://www.daowen.com)
解 (1)由运动方程
x=4t 2, y=2t+3
消去参数t可得
x=(y-3)2
此为抛物线方程,即质点的运动轨迹为抛物线。
(2)先将运动方程写成位置矢量形式:
r=x i+y j=4t 2i+(2t+3)j
t=0 s时,
r 0=3j m
t=1 s时,
r 1=(4i+5j)m
所以第1秒内的位移为
r=r 1-r 0=4i+5j-3j=(4i+2j)m
(3)由速度及加速度的定义得
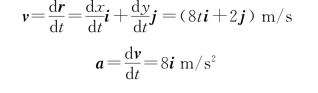
t=0 s时,
v=2j m/s, a=8i m/s2
t=1 s时,
v=(8i+2j)m/s, a=8i m/s2
(4)t=2 s时,
r=(16i+7j)m
所以前2 s内的平均速度为
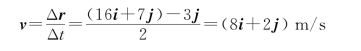
例1.4 通过绞车拉动湖中小船靠向岸边,如图1.6所示。如果绞车以恒定的速率u拉动纤绳,绞车定滑轮离水面的高度为h,求小船向岸边移动的速度和加速度。
解 设小船到绞车定滑轮的距离为l,任意时刻小船到岸边的距离x总满足x 2=l 2-h 2,两边对时间t求导数,得

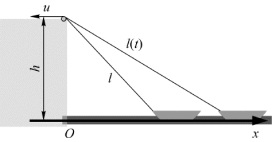
图1.6 例1.4用图
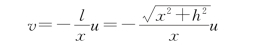
负号表示小船的速度沿x轴反方向。
小船向岸边移动的加速度为