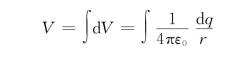5.5.5 等势面
前面曾用电场线描绘电场中各点场强的分布情况,从而对电场有比较形象直观的认识。同样,也可以用绘图的方法来描绘电场中电势的分布情况。
一般来说,静电场中的电势是逐点变化的,但场中有许多电势值相等的点,在静电场中把这些电势相等的点连起来形成的曲面(或平面)叫作等势面。场强和电势是描述静电场性质的两个基本物理量。场强的分布可以用电场线形象地表示,电势的分布则可以用等势面形象地表示。在电场中,由电势相等的点组成的曲面称为等势面。图5.29用虚线画出几种电场的等势面,实线表示电场线。
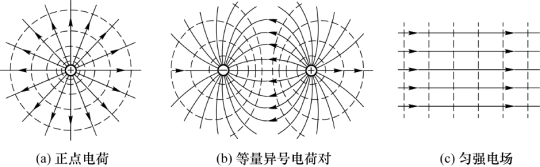
图5.29 几种电场的等势面
等势面有如下性质:
①在等势面上任意两点间移动电荷时,电场力做功为零;
②等势面与电场线处处正交;
③电场线总是从电势较高的等势面指向电势较低的等势面;
④若规定相邻两等势面的电势差相等,则等势面越密的地方,场强越大。
等势面是研究电场的一种极为有用的方法,许多实际电场(如示波管内的加速和聚焦电场)的电势分布往往不能表述成函数的形式,但可用实验的方法测出电场内等势面的分布,并根据等势面画出电场线,从而了解各处电场的强弱和方向。
![]()
1.两个重要的物理量
(1)电场强度E:
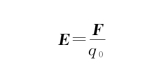
(2)电势V:
![]()
式中,a点电势为所求的电势,P 0为选定的参考点,该点的电势取为零(称零电势点)。电势是标量。
(3)电势差(也叫作电压):
![]()
电场中a、b两点的电势差在量值上等于单位正电荷从a点经过任意路径到达b点时电场力所做的功。故电荷q 0从a点移到b点时,静电场力所做的功为
A ab=W a-W b=q 0(V a-V b)(https://www.daowen.com)
2.两个基本定理
(1)高斯定理:
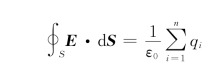
该定理说明,正电荷是电场的源头,负电荷是电场的尾闾。电力线总是从正电荷出发,到负电荷终止。静电场是有源场。
(2)环路定理:
![]()
该定理说明,场强沿任意闭合路径的线积分等于零,即静电场是保守力场,静电力是保守力。
3.场强与电势的积分关系
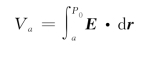
其中,P 0为零电势点。
4.求场强E和电势V的方法
(1)求场强面的方法,归纳为以下几种。
①直接积分法。任意一个带电体都可看成由许多点电荷组成的,写出一个点电荷(体元、面元或线元)的场强表达式,进行矢量积分,就可以求出整个带电体的场强。
②由高斯定理求解。当场强的分布具有高度对称性时,则可选取合适的高斯面来求解。
③灵活运用场的迭加原理,采用“挖补法”求不规则带电体的场强。
(2)求电势V的方法有以下几种。
①由场强的线积分求解:对有限带电体通常选“无限远”为参考点,所以![]() 。
。
注意:a.选择合适的积分路径:既然积分与路径无关,在我们选取积分路径时,总是设法选取使得计算比较简单的路径。
b.分段积分:由a到“无限远”。如果沿积分路径不同的区域内场强的函数关系不一样,则需分段进行积分。
②电势叠加法求解:利用点电荷电势公式,由电势的叠加原理进行标量积分求总电势。