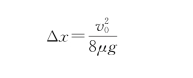4.2.2 质点系的动能定理
在讨论质点系的动能定理时,既要考虑外力的功,也要考虑内力的功。
设某系统有n个质点。对系统中第i个质点,外力做的功A外i=∫F外i·d r i,内力做的功A内i=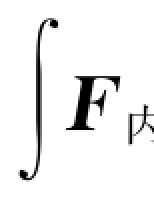
i·d r i,质点的动能从E k i1变化到E k i2,应用质点的动能定理得
再对系统中所有质点求和
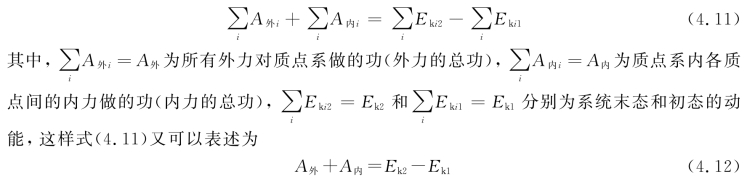
这个结论称作质点系的动能定理。它表明:所有外力对质点系做的功与内力做功之和等于质点系动能的增量。
质点系的动能定理指出,系统的动能既可以因为外力做功而改变,又可以因为内力做功而改变,这与质点系的动量定理和质点系的角动量定理不同,一对内力由于作用时间相同,其冲量之和必为零,又由于对同一参考点的力臂相同,其冲量矩之和也必为零,因此内力不改变系统总的动量和角动量。但是通过一对内力做功的讨论可知,它的做功并不一定为零(取决于两质点的相对位移),因此内力的功会改变系统的总动能。例如,飞行中的炮弹发生爆炸,爆炸前后系统的动量是守恒的,但爆炸后各碎片的动能之和必定远远大于爆炸前炮弹的动能,这就是爆炸时内力(炸药的爆破力)做功的结果。
一对内力特指两个物体之间的作用力和反作用力。一对内力的功是指在一个过程中作用力与反作用力做功之和(代数和),即总功。如果将彼此作用的两个物体视为一个系统,作用力与反作用力就是系统的内力。
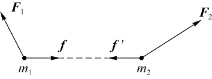
图4.8 一对内力的功
现在考虑系统内两个质点m 1和m 2,它们各自受到系统外的力F 1和F 2,如图4.8所示,它们之间有相互作用的内力f′和f,有f=-f′。在很短的时间Δt内,质点m 1在F 1和f的作用下移动Δr 1,同一时间内,质点m 2在F 2和f′的作用下移动Δr 2,则f对m 1做的功为A 1=f·Δr 1;f′对m 2做的功为A 2=f′·Δr 2,这一对内力做功之和为其中,Δr 12为m 1相对于m 2的位移。上式说明:一对内力的功(它们都为恒力)等于其中一个质点受的力与该质点对另一质点相对位移的点积(脚标1、2是可以交换的),即取决于力和相对位移。由于相对位移与参考系的选择没有关系,因此一对力做的总功与参考系的选择无关。根据这一特点,计算一对内力做功的时候,可以先假定其中的一个质点不动,另一个质点受力并沿着相对位移的路径运动,计算它相对移动时力做的功就行了。
A=A 1+A 2=f·Δr 1+f′·Δr 2=f·(Δr 1-Δr 2)=f·Δr 12
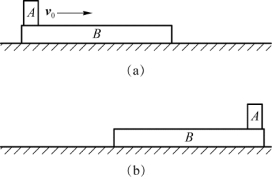
例4.2 质量为m B的木板静止在光滑桌面上,质量为m A的物体放在木板B的一端,现给物体A一初始速度v 0使其在B板上滑动,如图4.9(a)所示,设A、B之间的摩擦因数为μ,m A=m B,并设A滑到B的另一端时A、B恰好具有相同的速度,求B板的长度以及B板走过的距离。(A可视为质点。)
图4.9 例4.2用图
解 A向右滑动时,B给A一向左的摩擦力,A给B一向右的摩擦力,摩擦力的大小为μm Ag,将A、B视为一系统,摩擦力是内力,因此系统水平方向动量守恒。取向右为正,设A滑到B的右端时二者的共同速度为v,则
m Av 0=(m A+m B)v
解得
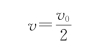
再对A、B系统应用质点系动能定理,注意到摩擦力的功是一对内力的功,可设B不动,A相对B移动了B的长度为L,摩擦力的功应为-μm Ag L,代入质点系动能定理
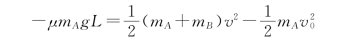
可得
为了计算B板走过的距离Δx,再单独对B板应用质点的动能定理,此时B板受的摩擦力做正功μm Ag·Δx,得
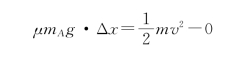
所以
