5.3.1 高斯定理
高斯(K.F.Gauss,1777—1855年)是德国物理学家和数学家,他在实验物理和理论物理以及数学方面都作出了很多贡献,他导出的高斯定理是电磁学的一条重要规律,是静电场有源性的完美数学表达。
高斯定理是用E通量表示的电场和场源电荷关系的定理,它给出了通过任意闭合曲面的E通量与闭合曲面内部所包围的电荷的关系。
高斯定理是静电学中的一个重要原理,下面我们分几步导出高斯定理。
(1)以点电荷q为球心,以任意半径r作一球面,计算通过该球面的电通量。
由于点电荷q的电场具有球对称性,球面上任一点场强E的量值都是E=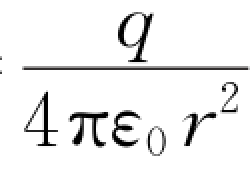 ,场强的方向都沿矢径方向,且处处与球面正交。如图5.14(a)所示,根据式(5.16)可求得通过球面的电通量为
,场强的方向都沿矢径方向,且处处与球面正交。如图5.14(a)所示,根据式(5.16)可求得通过球面的电通量为
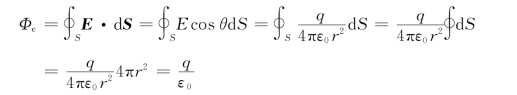
上式指出,点电荷q在球心时,通过任意球面的电通量都等于q/ε0,而与球面半径r的大小无关。
(2)通过包围点电荷q的任意闭合曲面S′的电通量。
如图5.14(a)所示,作任意闭合曲面S′,S′与球面S包围同一电荷q,根据电场线在没有电荷的地方不能中断的性质,容易看出,通过球面S和S′的电通量相等,都是q/ε0,由此证明了通过包围点电荷q的任意闭合曲面的电通量等于q/ε0,即
![]()
(3)闭合曲面外的点电荷,通过闭合曲面的电通量。
如图5.14(b)所示,点电荷q在闭合曲面外,在S面内没有其他电荷,由于电场线的连续性,有几条电场线穿入闭合曲面,必有几条电场线从闭合曲面内穿出,所以当点电荷q在闭合曲面外时,它通过该闭合面的电通量的代数和为零,即
![]()
应当指出,当点电荷位于闭合曲面外时,穿过闭合曲面的电通量虽然为零,但闭合曲面上各点处的场强E并不为零。(https://www.daowen.com)
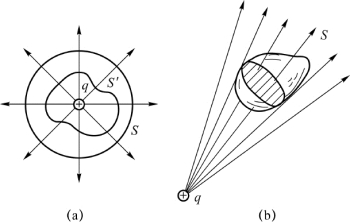
图5.14 高斯定理的说明
(4)点电荷系通过闭合曲面的电通量。
如果电场是由n个点电荷共同激发的,按电场强度的叠加原理,空间任意一点的电场强度是各个电荷(或电荷元)所激发的电场强度的叠加,即
E=E 1+E 2+E 3+…+E n
这时通过电场中任一闭合曲面S的电场强度通量为
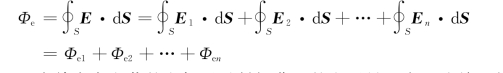
其中,Φe1,Φe2,…,Φe n为单个点电荷的电场通过封闭曲面的电通量。由上述关于单个点电荷的结论可知,当qi在封闭曲面内时,Φe i=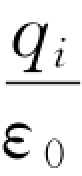 。当qi在封闭曲面外时,Φe i=0。所以上式可以写成
。当qi在封闭曲面外时,Φe i=0。所以上式可以写成

即在真空中,通过任一闭合曲面的电通量等于该面所包围的所有电荷的代数和除以ε0。这就是真空中的高斯定理。式(5.17)是高斯定理的数学表达式。
为了正确理解高斯定理,有必要指出以下几点。
①式(5.17)表明,通过闭合曲面的电通量仅是它所包围的电荷的贡献,与闭合曲面外的电荷无关。然而,闭合曲面上各点的场强E是闭合曲面内、外所有电荷产生的总场强。
②式(5.17)指出,当∑q in>0时,Φe>0表示有电场线从闭合面内穿出,故称正电荷为静电场的源头。当∑q in<0时,Φe<0,表示有电场线穿入闭合面内终止,故称负电荷为静电场的尾闾。因此,高斯定理表明电场线起始于正电荷,终止于负电荷,亦即静电场是有源场。
高斯定理不仅反映了静电场的性质,对于具有对称性的电场,用高斯定理计算场强可以避免复杂的积分运算。
