10.1.3 统计平均值
统计平均方法是统计学中常用的方法。
例如,计算某班学生大学物理成绩的统计平均值,设学生总人数为N,成绩为x 1的学生人数为ΔN 1,成绩为x 2的学生人数为ΔN 2,依此类推,则学生成绩的算术平均值为
![]()
利用概率的定义式(10.1),学生成绩的算术平均值可以写成
![]()
其中,Pi是学生成绩为x i的概率,也即成绩为x i的学生占学生总数的百分比。显然学生人数越多,学生成绩的算术平均值就越精确,算术平均值的极限就是统计平均值。
某一物理量M在一定条件下的可能取值为M 1,M 2,…,Mi,…,这些量称为随机变量。设随机变量M i出现的概率为P i,其统计平均值为
![]()
式(10.3)表明,物理量M是统计平均值为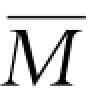 的某一取值M i乘以该值出现的概率P i,再对其乘积求和。或者说,物理量M的统计平均值为所有可能取值的概率与相应各取值M i的乘积的总和。
的某一取值M i乘以该值出现的概率P i,再对其乘积求和。或者说,物理量M的统计平均值为所有可能取值的概率与相应各取值M i的乘积的总和。
统计规律是对大量偶然事件整体起作用的规律,在研究大量事件(或一个事件的多次重复)时,单个事件虽然具有偶然性,但大量单个事件的整体行为却必然按一个确定的规律分布。
例如,计算压强时,对个别分子曾用了力学中的动量定理,但对大量分子的集体来说,个别分子作用在器壁上的瞬间冲量是无规则的、偶然的。而运用分子速度各向同性的统计假设求统计平均值的概念和方法则导致了一个有规律的压强值。
又如,在讨论气体分子速率分布时,某个分子具有多大速率是偶然的。在气体处于平衡态的条件下,只要气体中分子数目足够多,追踪个别分子由于分子间的碰撞而导致速度发生怎样的变化,这对系统性质的分析已不太重要。大量分子整体的速度分布遵循麦克斯韦定律。综上所述,统计规律性的一个特点是:个别分子的运动是偶然的、无规则的,但大量分子的整体行为却遵循必然的确定的规律。所以说,统计规律性是大量偶然事件的整体所表现的规律性。
