1.1.1 二阶行列式的概念
2026年01月14日
1.1.1 二阶行列式的概念
二元线性方程组的一般形式为

用消元法消去x2得
![]()
类似地,消去x1得
![]()
当a11a22-a12a21≠0时,得到该线性方程组的解:

从上面解的表达式可以看出,x1和x2的分母都是a11a22-a12a21,并且a11,a12,a21,a22是未知数x1和x2的系数.把这四个数按照顺序排成二行二列(横排称行,竖排称列)的数表并引进记号:
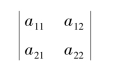
表示a11a22-a12a21的数值.
定义1.1.1
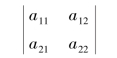 (https://www.daowen.com)
(https://www.daowen.com)
为两行两列的数表,称为二阶行列式,其值等于a11a22-a12a21.
称aij(1≤i,j≤2)为行列式的元素,第一个下标i表示行标,表示该元素在第i行,第二个下标j表示列标,表示该元素在第j列.例如a21在第2行第1列.
二阶行列式表示的代数和可以用图1.1来帮助记忆.
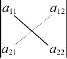
图1.1
在二阶行列式中,把a11到a22的对角连线称为主对角线,把a12到a21的对角连线称为副对角线.二阶行列式的值等于其主对角线(实线)上的两个元素之积减去副对角线(虚线)上的两个元素之积.即
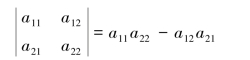
二阶行列式的这种计算方法又称为对角线法则.
利用二阶行列式的概念,式(1.2)中x1,x2的分子也可以写成
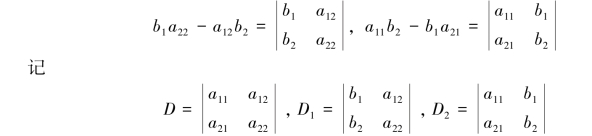
则式(1.2)可以写成
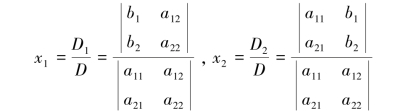
其中,D是由方程组的系数位置顺序不变确定的二阶行列式,称为系数行列式;D1是用b1,b2替换D中第一列得到的行列式;D2是用b1,b2替换D中第二列得到的行列式.
