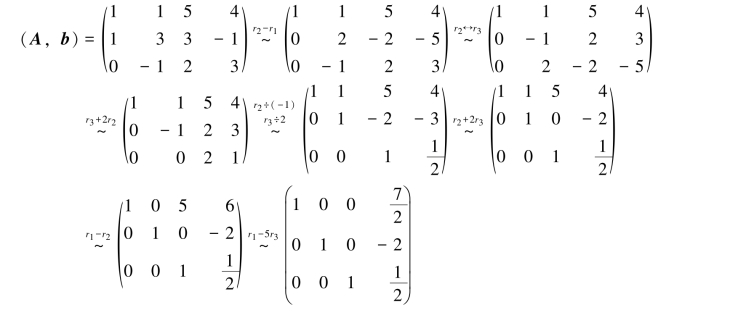3.7.3 向量空间的基、维数和坐标
定义3.7.3 V为一个向量空间,如果向量组α1,α2,…,αr∈V满足:
(1)α1,α2,…,αr线性无关;
(2)V中任意一个向量都可由向量组α1,α2,…,αr线性表示.则向量组α1,α2,…,αr称为向量空间V的一个基,r称为向量空间V的维数,并称V为r维向量空间.
向量空间实际上就是一个满足加法封闭和数乘封闭的向量组,由α1,α2,…,αs生成的向量空间V的基就是向量组α1,α2,…,αs的最大无关组,V的维数就是向量组α1,α2,…,αs的秩,由于向量组的最大线性无关组不唯一,因此向量空间的基也不唯一.
显然,零空间{0}没有基,维数为0.
定义3.7.4 设V为一个向量空间,α1,α2,…,αr为V的基,如果满足:
(1)‖αi‖=1(i=1,2,…,r);
(2)α1,α2,…,αr两两正交.
则称α1,α2,…,αr为V的规范正交基.
由定义知,规范正交基形成的矩阵一定是正交矩阵.
由定理3.3.5可得如下定理.
定理3.7.3 n维向量空间V的任意一个向量用V的一个基线性表出时,其表示法是唯一的.
定义3.7.5 令α1,α2,…,αn是向量空间V的一个基,那么V中任意向量β可唯一表示为
那么,称n元有序数组k1,k2,…,kn是β在基α1,α2,…,αn下的坐标(或β关于基α1,α2,…,αn的坐标).
在Rn中,n维单位向量
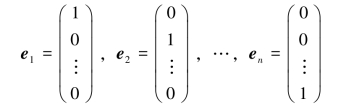
就是n维向量空间Rn的一个规范正交基,它们两两正交,且都是单位向量.
例3.7.5 在R4中,求由向量组a1=(1,3,2,0)T,a2=(7,0,14,3)T,a3=(1,-4,2,1)T,a4=(2,-1,4,1)T所生成的向量空间V的基及维数.
解 由a1,a2,a3,a4生成的向量空间V的基就是向量组a1,a2,a3,a4的最大线性无关组,知V的维数就是向量组a1,a2,a3,a4的秩.计算如下:
解 要证a1,a2,a3是R3的一个基,只要证a1,a2,a3线性无关,即只要证A~E.又设
对矩阵(A,b)施行初等行变换,若A能变为E,则a1,a2,a3为R3的一个基,且当A变为E时,x=A-1b即为b在这个基中的坐标.计算如下:
