5.3.2　实对称矩阵的正交相似对角化.

5.3.2　实对称矩阵的正交相似对角化.

定理5.3.4　设A为n阶对称矩阵,则必有n阶正交矩阵P,使P-1AP=PTAP=Λ,其中,Λ是以A的n个特征值为对角元的对角阵.

根据定理5.3.4,一定存在一个正交相似变换矩阵使对称矩阵实现对角化.

对称矩阵A对角化的步骤如下:

(1)求出方阵A的全部互异的特征值λ1,λ2,…,λs,它们的重数依次为k1,k2,…,ks(k1+k2+…+ks=n).

(2)对求得的每个ki重特征值λi,求齐次线性方程组(A-λiE)x=0的基础解系,得到ki个线性无关的特征向量,再把它们正交化、单位化,得到ki个两两正交的单位特征向量.因为k1+k2+…+ks=n,所以总共可得n个两两正交的单位化的特征向量.

(3)把这n个两两正交的单位特征向量,与对角元的排列次序相对应,依次排列构成正交矩阵P,便有P-1AP=PTAP=Λ.

求得A的特征值为λ1=-2,λ2=λ3=1.

对应λ1=-2,解方程(A+2E)x=0,由

将p1,p2,p3构成正交矩阵:

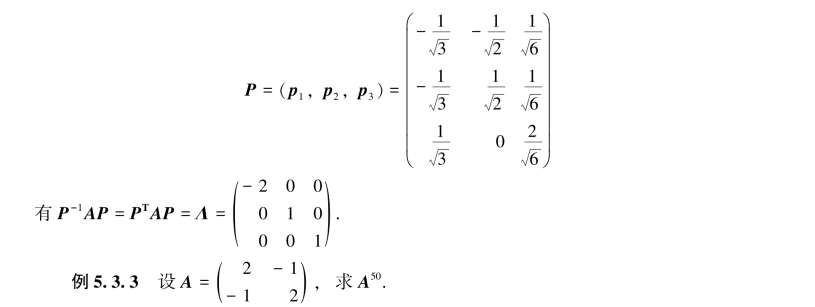
解　因A对称,故A可对角化,即有可逆矩阵P及对角阵Λ,使P-1AP=Λ.于是A=PΛP-1,从而A50=PΛ50P-1.

由