3.4.4 向量组的秩的几何意义及应用
2026年01月14日
3.4.4 向量组的秩的几何意义及应用
下面用几何方法在R3中寻找向量组的最大无关组,进而求出向量组的秩.
如图3.5所示,首先在空间的四条直线上各自画出一个向量,得到向量组α1,β1,η1,γ1,然后,把共面的三个向量α1,β1,η1留下两个β1,η1,与另外一个不共面的向量组成向量组β1,η1,γ1,如图3.6所示,即得到向量组α1,β1,η1,γ1的最大无关组β1,η1,γ1,且向量组的秩为3.
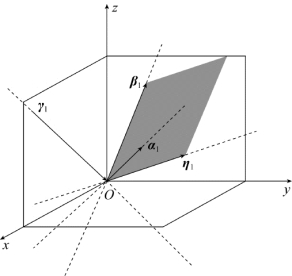
图3.5(https://www.daowen.com)
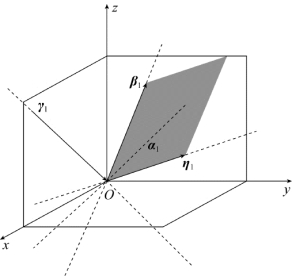
图3.6
最大无关组的概念不止存在于向量组里面,现实生活中,最大无关组无处不在.举例而言,从理论上讲,自然界中任何色彩均可由三种基色(红、绿、蓝)按不同比例混合得到;反之,任意一种色彩均可被分解为三种基色.那么红、绿、蓝这三种基色实际上就可以看成所有颜色组成集合的一个“最大无关组”;任何一种色彩都可以表示成三种基色的“线性组合”.然而,人们又发现,作为基色的三种色彩并不是唯一的,但它们之间要相互独立(无关),即其中任何一种基色都不能由另外两种基色混合来产生,这从某种意义下又印证了“最大无关组”的不唯一性.
