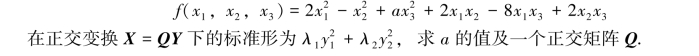同步习题

同步习题

一、填空题.(每小题4分,共20分)

1.设n阶矩阵A可逆,k为常数,m为正整数,λ是A的特征值,则A-1的特征值为________;Am的特征值为________;A*(A的伴随矩阵)的特征值为________;矩阵A的多项式φ(A)=a0E+a1A+…+amAm的特征值为____________________.

5.(2008,数一)设A为二阶矩阵,a1,a2为线性无关的二维列向量,Aa1=0,Aa2=2a1+a2,则A的非零特征值为____________________.

二、选择题.(每小题4分,共20分)

1.设A为n阶方阵,则以下结论正确的是(　　).

(A)若A可逆,则A的对应于特征值λ的特征向量也是A-1的对应于特征值的特征向量

(B)A的特征向量的任一线性组合仍是A的特征向量

(C)A与AT具有相同的特征向量

(D)A的特征向量为方程组(A-λE)x=0的全部解向量

2.若A既是正交矩阵又是正定矩阵,则A=(　　).

(A)A2　(B)2A　(C)E　(D)2E

六、(每小题5分,共10分)求出下列每个二次型化为标准形的正交变换,并写出标准形:

九、(10分)设A为3阶实对称矩阵,且满足A2+2A=O.已知A的秩R(A)=2.(1)求A的全部特征值;(2)当k为何值时,A+kE为正定矩阵?

十、(2017,数三,10分)设二次型