2.3.2　逆矩阵的性质

2.3.2　逆矩阵的性质

推论2.3.1　若AB=E(或BA=E),则B=A-1.

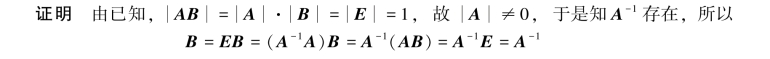
方阵的逆矩阵满足下列运算规律:

(1)若A可逆,则A-1也可逆,且(A-1)-1=A;

(3)若A、B为同阶可逆矩阵,则AB也可逆,且(AB)-1=B-1A-1;

(4)若A可逆,则AT也可逆,且(AT)-1=(A-1)T.

证明　因为AT(A-1)T=(A-1A)T=ET=E,所以(AT)-1=(A-1)T.

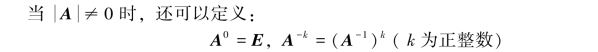
这样,当A可逆时,有

于是得到

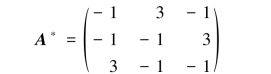
故由式(2.17)可得

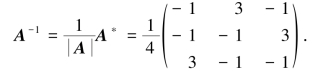
我们指出对角矩阵可逆的充要条件:其所有对角线元素非零并且

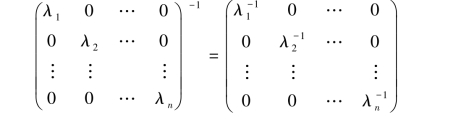
副对角矩阵可逆的充要条件:其所有副对角线元素非零并且

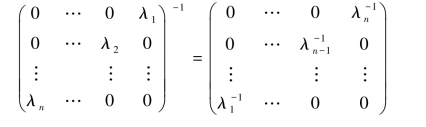(https://www.daowen.com)

例2.3.2　已知

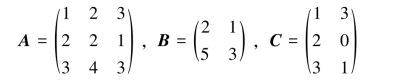
求矩阵X,使得AXB=C.

解　若A-1,B-1都存在,则用A-1左乘上式、B-1右乘上式,得

即

故

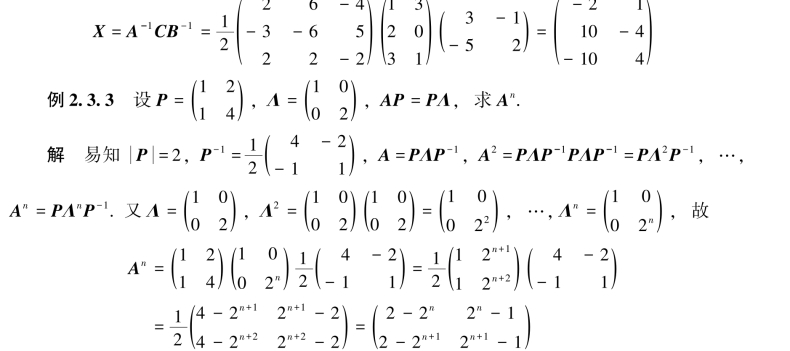
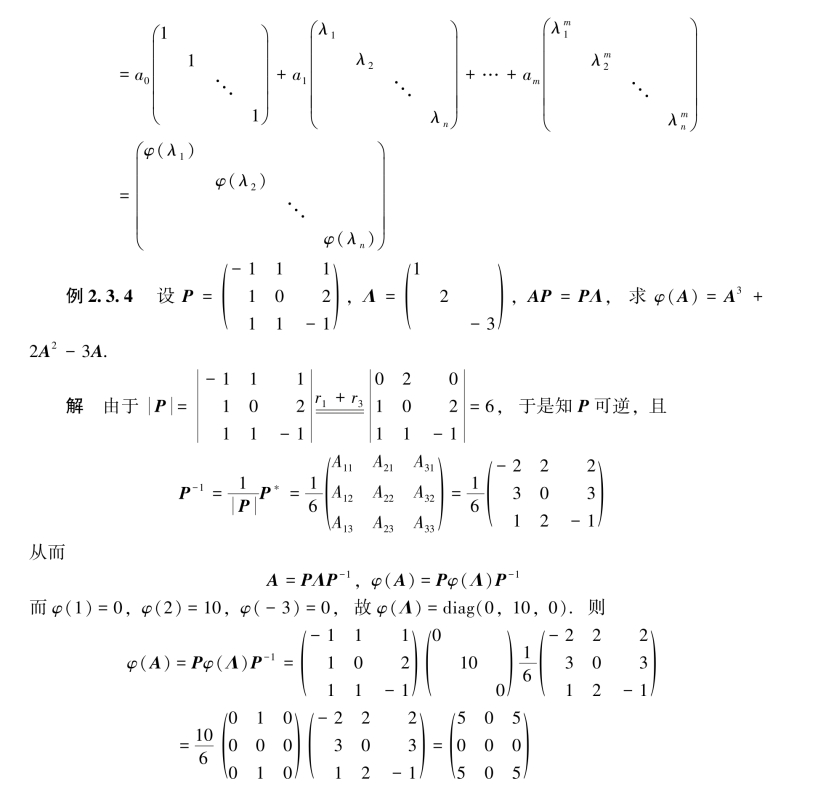
设φ(x)=a0+a1x+…+amxm为x的m次多项式,A为n阶矩阵,记

φ(A)称为矩阵A的m次多项式.

因为矩阵Ak,Al和E都是可交换的,所以矩阵A的两个多项式φ(A)和f(A)总是可交换的,即总有

从而A的几个多项式可以像数x的多项式一样相乘或分解因式.例如:

我们常用例2.3.3中计算Ak的方法来计算A的多项式φ(A),即

(1)若A=PΛP-1,则Ak=PΛkP-1,从而