3.4.3 向量组的秩和矩阵的秩的关系
定义3.4.2 矩阵的行向量组的秩称为矩阵的行秩,矩阵的列向量组的秩称为矩阵的列秩.
定理3.4.3 设A为m×n矩阵,则矩阵A的秩等于它的列秩,也等于它的行秩.
证明 设矩阵A的秩为r,则
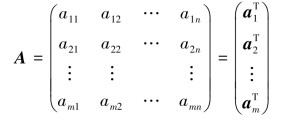
设矩阵A经过初等行变换化为
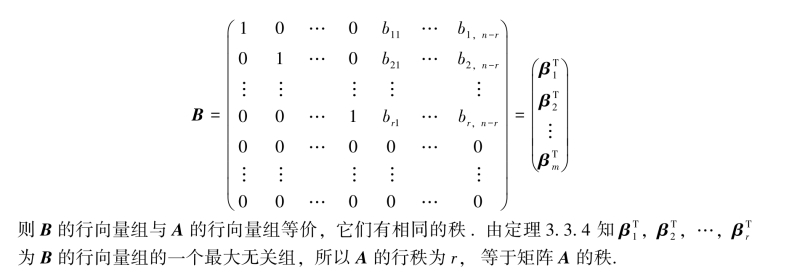
同理可证,矩阵A的列秩等于矩阵A的秩.
由定理3.4.3及定理3.3.4可知,若Dr是矩阵A的一个最高阶非零子式,则Dr所在的r列就是A的列向量组的一个最大无关组;Dr所在的r行就是A的行向量组的一个最大无关组.

证明 设A经过有限次初等行变换化为矩阵B,所以,必有可逆矩阵P使PA=P(α1,α2,…,αn)=B=(β1,β2,…,βn),显然,A和B等价.根据第二章定理2.6.1知,A和B有相同的秩.设有一组实数k1,k2,…,kn∈R,使得
![]()
即
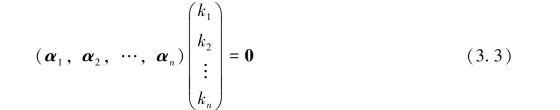
两端同时左乘矩阵P得
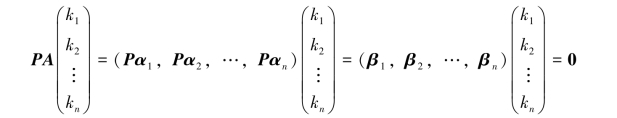
由k1β1+k2β2+…+knβn=0可知,A的列向量组和B的列向量组具有相同的线性相关性.
因此,如果A的列向量组中有某种线性组合关系,B相对应的列向量组也具有相同的线性组合关系.因为P是可逆矩阵,所以如果可以知道B的列向量组具有某种线性组合关系,则A中相对应的列向量组也有这种线性组合关系.
根据上述结论,一个列向量组组成矩阵后,将矩阵用初等行变换化为行阶梯形矩阵,通过确定行阶梯形中最高阶非零子式所在的列,不仅可以得到列向量组的一个最大线性无关组,同时,还可以把其余列向量用该最大无关组线性表出.
根据定理3.4.4,原矩阵中对应的列向量组和行阶梯形矩阵的列向量组具有相同的线性组合关系,相应地,可以对应得到所求的列向量组的一个最大线性无关组,并把其余列向量用该最大无关组线性表出.
同理,一个行向量组组成矩阵后,通过初等列变换,也可以求出行向量组的最大无关组.
例3.4.1 设矩阵

求矩阵A的秩及A的列向量组的一个最大无关组,并把不属于最大无关组的其余列向量用最大无关组线性表示.
解 对A施以初等行变换变为行阶梯形矩阵,即

知R(A)=3,故A的列向量组的一个最大无关组含3个向量.从矩阵B可以确定一个最高阶非零子式所在列为矩阵中的第1,2,4列,根据定理3.4.4,知A的列向量组的一个最大无关组为α1,α2,α4.这是因为
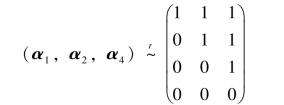
知R(α1,α2,α4)=3,故α1,α2,α4线性无关.
为了把α3,α5用α1,α2,α4线性表示,只需用初等行变换继续把A化为行最简形矩阵:(https://www.daowen.com)
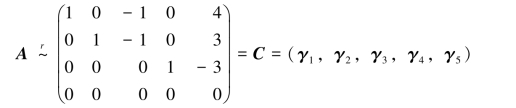
由于方程组Ax=0与Cx=0同解,因此向量α1,α2,α3,α4,α5之间的线性关系与向量γ1,γ2,γ3,γ4,γ5之间的线性关系是相同的,显然,从矩阵C中可以看出列向量组具有线性组合关系:
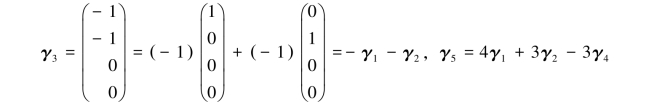
由定理3.4.4,知α3=-α1-α2,α5=4α1+3α2-3α4.
定理3.4.5 若向量组A:a1,a2,…,am能由向量组B:b1,b2,…,bn线性表示,则R(a1,a2,…,am)≤R(b1,b2,…,bn).
证明 不妨设a1,a2,…,am的最大无关组为a1,a2,…,as;b1,b2,…,bn的最大无关组为b1,b2,…,bt,由定理3.4.2知a1,a2,…,as能由b1,b2,…,bt线性表出.则b1,b2,…,bt为向量组C:a1,a2,…,as,b1,b2,…,bt的最大无关组,即向量组C的秩为t,而a1,a2,…,as为向量组C的部分组,故s≤t,即R(a1,a2,…,am)≤R(b1,b2,…,bn).
推论3.4.1 等价的向量组的秩相等.
证明 设向量组A:a1,a2,…,am与向量组B:b1,b2,…,bn等价,a1,a2,…,am的最大无关组为ai1,ai2,…,ais.
由已知条件ai1,ai2,…,ais与b1,b2,…,bn等价,根据定理3.4.1知,ai1,ai2,…,ais为b1,b2,…,bn的最大无关组,所以R(a1,a2,…,am)=R(b1,b2,…,bn)=s.
推论3.4.2 若向量组a1,a2,…,as线性无关,且可被b1,b2,…,bt线性表出,则s≤t.
推论3.4.3 若向量组a1,a2,…,as可被b1,b2,…,bt线性表出,且s>t,则a1,a2,…,as线性相关.
推论3.4.4 设向量组B是向量组A的部分组,若向量组B线性无关,且向量组A能由向量组B线性表示,则向量组B是向量组A的一个最大无关组.
定理3.4.6 向量组B:b1,b2,…,bs能由向量组A:a1,a2,…,at线性表示的充分必要条件是矩阵A=(a1,a2,…,at)的秩等于矩阵(A,B)=(a1,a2,…,at,b1,b2,…,bs)的秩,即
![]()
推论3.4.5 设A=(a1,a2,…,at),B=(b1,b2,…,bs),(A,B)=(a1,a2,…,at,b1,b2,…,bs),向量组A:a1,a2,…,at与向量组B:b1,b2,…,bs等价的充分必要条件是R(A)=R(B)=R(A,B).
证明 由已知条件知,向量组A与向量组B等价.所以,向量组A与向量组B可以互相线性表示,由定理3.4.6知
![]()
由R(A,B)=R(B,A),得向量组A与向量组B等价的充分必要条件是
![]()
例3.4.2 设向量组B能由向量组A线性表示,且它们的秩相等,证明向量组A与向量组B等价.
证明 设向量组A和向量组B合并成向量组C,因为向量组B能由向量组A线性表示,
由定理3.4.6知R(A)=R(C),又已知R(A)=R(B),故有R(A)=R(B)=R(C),由推论3.4.5知,向量组A与向量组B等价.
例3.4.3 已知向量组
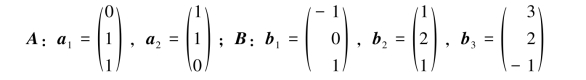
证明向量组A与向量组B等价.
证明 记A=(a1,a2),B=(b1,b2,b3),(A,B)=(a1,a2,b1,b2,b3),由推论3.4.5知,只需证R(A)=R(B)=R(A,B).易知
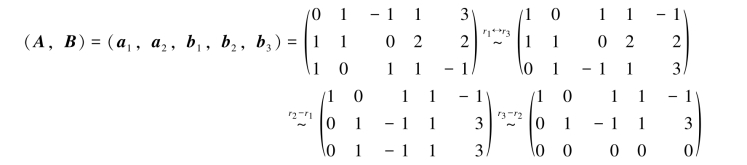
所以,R(A)=R(B)=R(A,B),即向量组A与向量组B等价.
