2.7.2　线性方程组的有解判别定理

2.7.2　线性方程组的有解判别定理

定理2.7.1　n元齐次线性方程组Am×nx=0有非零解的充要条件是系数矩阵的秩R(A)＜n.

证明　必要性.设方程组Ax=0有非零解.

设R(A)=n,则在A中应有一个n阶非零子式Dn.根据克拉默法则,Dn所对应的n个方程只有零解,则原方程组只有零解与假设矛盾,故R(A)＜n.

充分性.设R(A)=r＜n,则A的行阶梯形矩阵只含有r个非零行,把这r行的第一个非零元所对应的未知量作为非自由量,其余n-r个作为自由未知量(即可取任意实数的未知量).任取一个自由未知量为1,其余自由未知量为0,即可得到方程组的一个非零解.

定理2.7.2　n元非齐次线性方程组Am×nx=b有解的充分必要条件:它的系数矩阵A的秩与增广矩阵B的秩相等,即R(A)=R(B).

证明　必要性.设方程组Ax=b有解,但R(A)＜R(B),则B的行阶梯形矩阵中最后一个非零行对应矛盾方程0=1,这与方程组有解相矛盾.故R(A)=R(B).

充分性.若A与B的秩相等,设R(A)=R(B)=r,则B的行阶梯形矩阵中含有r个非零行,把这r行的第一个非零元所对应的未知量作为非自由量,其余n-r个作为自由未知量,并令这n-r个自由未知量全为零,即可得到方程组的一个解.

此定理可推广到矩阵方程.

推论2.7.1　矩阵方程Ax=b有解的充分必要条件是R(A)=R(A,B).

证明　设A为m×n矩阵,B为m×l矩阵,则X为n×l矩阵.把X和B按列分块,记为

则矩阵方程Ax=b等价于l个向量方程:

由定理2.7.2可得

Ax=b有解⇔Axi=bi有解(i=1,2,…,l);

利用推论2.7.1,容易得出矩阵的秩的性质(7),即

定理2.7.3　设n元线性方程组Ax=b,则该方程组:

(1)无解的充分必要条件是R(A)＜R(B);

(2)有唯一解的充分必要条件是R(A)=R(B)=n;

(3)有无穷多解的充分必要条件是R(A)=R(B)＜n.

解　对系数矩阵A进行初等行变换,化为行最简形矩阵

解　对增广矩阵B进行初等行变换,得

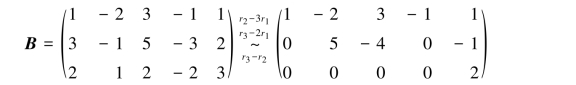
显然,R(A)=2,R(B)=3,故方程组无解.

例2.7.3　判断下列线性方程组是否有解?如有解,是否有唯一的解?

把x3,x4移到等号的右边,得

由于参数c1,c2可任意取值,故方程组(2.32)有无穷多个解,进而方程组(2.31)有无穷多个解.

(1)当p≠2时,R(A)=R(B)=4,方程组有唯一解;

(2)当p=2时,有

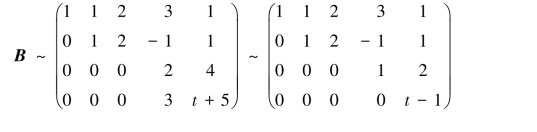
当t≠1时,R(A)=3＜R(B)=4,方程组无解;

当t=1时,R(A)=R(B)=3,方程组有无穷多解.则