同步习题
一、填空题.(每小题4分,共20分)

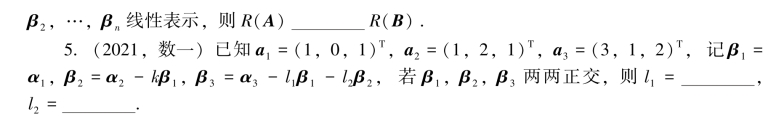
二、选择题.(每小题4分,共20分)
1.设两个向量组A与B的秩相等,且A可由B线性表出,则( ).
(A)B可由A线性表出 (B)B不一定能由A线性表出
(C)A线性无关 (D)A的向量的个数多于B的向量的个数
![]()
(A)存在一组全为零的数k1,k2,…,ks,使得k1 a1+k2 a2+…+ks as=0
(B)a1,a2,…,as中任意两个向量都线性无关
(C)a1,a2,…,as中存在一个向量,它不能由其余向量线性表示
(D)a1,a2,…,as中任意一个向量都不能由其余向量线性表示
3.已知向量组a1=(1,k1,0,0)T,a2=(1,k2,2,0)T,a3=(1,k3,2,3)T,a4=(1,k4,0,3)T,则对任意数ki(i=1,2,3,4),必有( ).
(A)a1,a2,a3线性相关(B)a1,a2,a3线性无关
(C)a1,a2,a3,a4线性相关(D)a1,a2,a3,a4线性无关
4.设向量组a1,a2,a3线性无关,则下列向量组线性相关的是( ).
(A)a1-2a2,a2-2a3,a3-2a1(B)a1+a2,a2+a3,a3+a1
(C)a1-a2,a2-a3,a3-a1(D)a1+2a2,a2+2a3,a3+2a1
5.(2013,数一)设A,B,C均为n阶矩阵,若AB=C,且B可逆,则( ).(https://www.daowen.com)
(A)矩阵C的行向量组与矩阵A的行向量组等价
(B)矩阵C的列向量组与矩阵A的列向量组等价
(C)矩阵C的行向量组与矩阵B的行向量组等价
(D)矩阵C的列向量组与矩阵B的列向量组等价
三、计算题.(每小题5分,共10分)
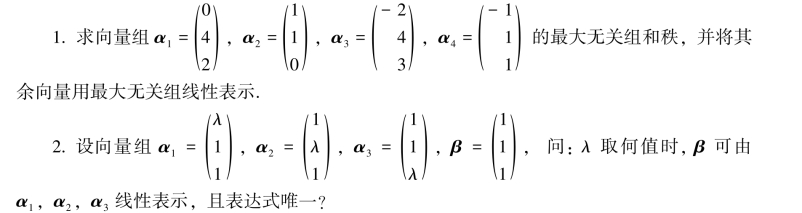
四、证明题.(每小题5分,共20分)
1.设A是n阶方阵,α是n维列向量,若An-1α≠0,而Anα=0,证明α,Aα,…,An-1α线性无关.
2.设向量组a1,a2,…,an(n≥2)线性无关,并且bi=ai+li an(i=1,2,…,n-1),证明向量组b1,b2,…,bn-1线性无关.
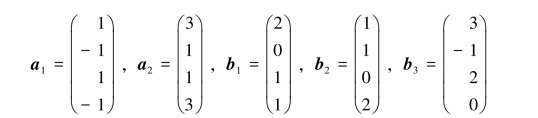
3.设证明向量组a1,a2与向量组b1,b2,b3等价.
4.由a1=(1,1,0,0)T,a2=(1,0,1,1)T所生成的向量空间记作L1,由b1=(2,-1,3,3)T,b2=(0,1,-1,-1)T所生成的向量空间记作L2,试证明L1=L2.
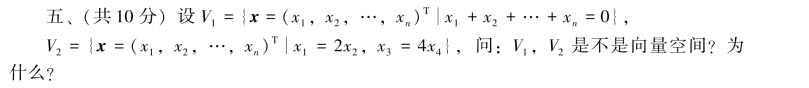
六、(2006,数三)(共10分)设四维向量α1=(1+a,1,1,1)T,α2=(2,2+a,2,2)T,α3=(3,3,3+a,3)T,α4=(4,4,4,4+a)T,问:a为何值时,α1,α2,α3,α4线性相关?当α1,α2,α3,α4线性相关时,求其一个最大无关组,并将其余向量用最大无关组线性表示.
七、(共10分)设α1,α2,α3为向量空间R3的一个基,β1,β2,β3与γ1,γ2,γ3为R3中两个向量组,且
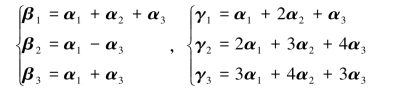
(1)验证β1,β2,β3及γ1,γ2,γ3都是R3的基;
(2)求由β1,β2,β3到γ1,γ2,γ3的过渡矩阵;
(3)求由β1,β2,β3中坐标到γ1,γ2,γ3中坐标的变换公式.
