4.1.1　齐次线性方程组解的性质

4.1.1　齐次线性方程组解的性质

设n元齐次线性方程组:

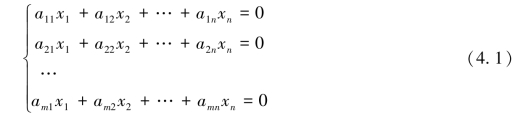
令

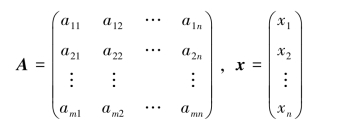
显然,齐次线性方程组(4.1)可写成矩阵方程:

齐次线性方程组总是有解,xi=0(i=1,2,…,n)就是它的一个解,称为零解.对齐次线性方程组,主要是关心它在什么条件下有非零解,以及如何求出它的全部非零解.

在第2.7节线性方程组的有解判定定理中已介绍,n个未知数的齐次线性方程组Ax=0有非零解的充分必要条件是系数矩阵的秩R(A)＜n.为了研究齐次线性方程组解的结构,先讨论这些解的性质,并给出基础解系的概念.

若x1=ξ11,x2=ξ21,…,xn=ξn1为方程组(4.1)的一个解,则

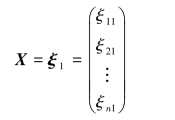
称为方程组(4.1)的解向量,它也是矩阵方程(4.2)的解.

性质4.1.1　若ξ1,ξ2为方程(4.2)的解,则X=ξ1+ξ2也是方程(4.2)的解.

证明　只要验证X=ξ1+ξ2满足方程(4.2)即可.

因为A(ξ1+ξ2)=Aξ1+Aξ2=0+0=0,所以X=ξ1+ξ2也是方程(4.2)的解.

性质4.1.2　若ξ1为方程(4.2)的解,k为实数,则x=kξ1也是方程(4.2)的解.

证明　只要验证x=kξ1满足方程(4.2)即可.易知A(kξ1)=k(Aξ1)=k0=0.证毕.