2.5.2 初等矩阵
定义2.5.3 由单位阵E经过一次初等变换而得到的矩阵,称为初等矩阵.
三种初等变换对应有三种初等矩阵.
1)对调两行或对调两列
把单位阵中第i、j两行对调(ri↔rj),得初等矩阵

用m阶初等矩阵Em(i,j)左乘矩阵A=(aij)m×n,得
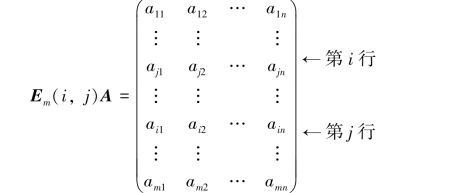
其结果相当于对矩阵A施行第一种初等行变换:把A的第i行与第j行对调(ri↔rj).类似地,以n阶初等矩阵En(i,j)右乘矩阵A,其结果相当于对矩阵A施行第一种初等列变换:把A的第i列与第j列对调(ci↔cj).
2)以数k≠0乘某行或某列
以数k≠0乘单位矩阵的第i行(ri×k),得初等矩阵

可验证,以Em[i(k)]左乘矩阵A,其结果相当于以数k乘A的第i行(ri×k);以En[i(k)]右乘矩阵A,其结果相当于以数k乘A的第i列(ci×k).
3)以数k乘某行(列)加到另一行(列)上去
以数k乘E的第j行加到第i行上(ri+krj),或以k乘E的第i列加到第j列上(cj+kci),得初等方阵

可验证,以Em[i+j(k)]左乘矩阵A,其结果相当于把A的第j行乘k加到第i行上(ri+krj);以En[i+j(k)]右乘矩阵A,其结果相当于把A的第i列乘k加到第j列上(cj+kci).
综上所述,可得以下性质.
性质2.5.1 设A是一个m×n矩阵,对A施行一次初等行变换,相当于在A的左边乘以相应的m阶初等矩阵;对A施行一次初等列变换,相当于在A的右边乘以相应的n阶初等矩阵.
初等变换对应初等矩阵.因为初等矩阵是方阵且其行列式不等于零,所以是可逆的.也可以由初等变换可逆知初等矩阵也可逆,且该初等变换的逆变换也就对应该初等矩阵的逆阵.(https://www.daowen.com)
定理2.5.1 初等矩阵是可逆矩阵,且
(1)E(i,j)-1=E(i,j);

推论2.5.1 方阵A可逆的充分必要条件是存在有限个初等矩阵P1,P2,…,Pl,使得A=P1P2…Pl.
证明 先证充分性.设A=P1P2…Pl,由于初等矩阵可逆,有限个可逆矩阵的乘积仍可逆,故A可逆.
再证必要性.设n阶方阵A可逆,且A的标准形矩阵为F,由F~A可知,F经有限次初等变换可化为A,即存在有限个初等矩阵P1,P2,…,Pl,使得
![]()
又由于A可逆,P1,P2,…,Pl也都可逆,于是标准形矩阵F也可逆.假设

定理2.5.2 设A与B为m×n矩阵,那么

类似可证明(2)和(3).

因此若对矩阵(A,E)施行初等行变换,则当把A变成B时,E就变成了P,从而就得到了所求的可逆矩阵P.


解 设可逆矩阵P使PA=F为行最简形矩阵,则有

为方程的唯一解.
