3.5.1　向量的内积、长度、夹角的定义

3.5.1　向量的内积、长度、夹角的定义

定义3.5.1　设有n维向量

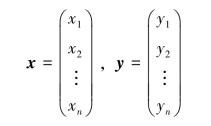
称

为向量x与y的内积,记作[x,y].

内积是两个向量之间的一种运算,其结果是一个数.内积可以用矩阵运算关系表出,当向量x与y都是列向量时,有

内积满足以下运算规律(x,y,z为n维向量,λ为实数):

(1)[x,y]=[y,x];

(2)[λx,y]=[x,λy]=λ[x,y];

(3)[x+y,z]=[x,z]+[y,z];

(4)[x,x]≥0,[x,x]=0⇔x=0;

(5)[x,y]2≤[x,x][y,y](施瓦兹(Schwarz)不等式).

n维向量的内积是解析几何中数量积概念的推广.但是,n(n＞3)维向量没有3维向量那样直观的长度和夹角的概念.数学家威廉·金登·克利福德(William Kingdon Clifford)指出:“我们已有的空间科学所研究的问题是在特定的三维空间中的距离关系.但是,这不意味着在高于三维的空间中不存在距离关系”.因此,可以按照数量积的直角坐标计算公式进行推广,用内积定义n维向量的长度和夹角.

定义3.5.2　令

‖x‖称为n维向量x的长度或范数.当‖x‖=1时,称x为单位向量.

向量的长度有以下性质.

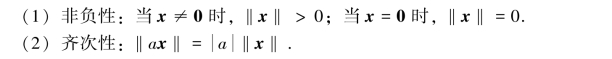
(3)三角不等式:‖x+y‖≤‖x‖+‖y‖.

定义3.5.3　设x≠0,y≠0,定义x与y的夹角为

若[x,y]=0,则称向量x与y正交.显然,零向量与任何向量都正交.