3.5.2 正交向量组
定义3.5.4 设a1,a2,…,as是一组非零向量,若该向量组中任意两个向量都正交,则称a1,a2,…,as为正交向量组.
定义3.5.5 设e1,e2,…,es是一组正交向量组,且每一个向量都是单位向量,称e1,e2,…,es为规范正交向量组.
定理3.5.1 非零正交的向量组必线性无关.
证明 设a1,a2,…,as为一非零正交的向量组,令
以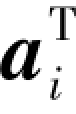
左乘上式两端,由已知[ai,aj]=0,i≠j,故得
因为ai≠0,所以ki=0(i=1,2,…,s),即a1,a2,…,as线性无关.
例3.5.1 已知3维空间中两个向量
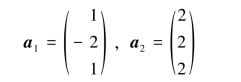
正交,试求一个非零向量a3使a1,a2,a3两两正交.
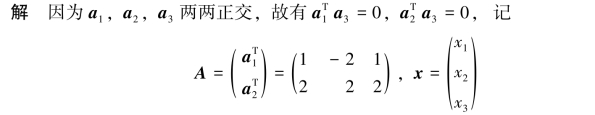
则a3应满足齐次线性方程组Ax=0,即
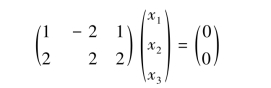
由
