同步习题
一、填空题.(每小题4分,共20分)
1.全体正实数的集合R+,对于加法和纯量乘法:a⊕b=ab,k°a=ak,构成R上的线性空间,此空间的零元素是________;a∈R+的负元素为________.
2.设P[x]2是次数小于等于2的全体多项式与零多项式组成的线性空间,则多项式p=2x2-5x+6在基p1=1,p2=x-1,p3=(x-1)2下的坐标为________.
3.R2×2是全体二阶实矩阵构成的线性空间,该线性空间的自然基底为________.
4.在线性空间V中,定义T(α+η)=α+η,其中α是V中任意向量,η≠0是V中一个固定的向量,此变换________线性变换(填“是”或“不是”).
5.在R3中线性变换T(x1,x2,x3)=(2x1-x2,x2+x3,x1),那么T关于基e1=(1,0,0),e2=(0,1,0),e3=(0,0,1)的矩阵是________.
二、选择题.(每小题4分,共20分)
1.下列各向量集合构成的是线性空间的是( ).
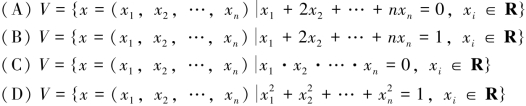
2.全体四阶上三角形矩阵对于矩阵的加法和数乘构成的线性空间是( ).
(A)4维的 (B)8维的 (C)10维的 (D)16维的
3.下列集合构成Rn的子空间的是( ).
(A)分量是整数的所有n维向量
(B)第1、2两个分量相等的所有n维向量
(C)三维空间中,终点不位于一给定直线上的所有向量
(D)各分量之和不等于1的所有n维向量
4.下列命题正确的是( ).
(A)设α1,α2,…,αn是线性空间V中n个向量,且V中每个向量都可由α1,α2,…,αn线性表示,则α1,α2,…,αn是V的一个基
(B)设α1,α2,…,αn是线性空间V中的一个基,若β1,β2,…,βn与α1,α2,…,αn等价,那么β1,β2,…,βn也是V的一个基
(C)T是线性空间V的线性变换,向量组α1,α2,…,αn线性相关,那么T(α1),T(α2),…,T(αn)也线性相关
(D)在取定基后,V的每个可逆线性变换对应于可逆矩阵,但逆变换未必对应于逆矩阵(https://www.daowen.com)
5.线性变换T在基α1,α2,…,αn与β1,β2,…,βn下的矩阵分别是A与B,并且有(β1,β2,…,βn)=(α1,α2,…,αn)C,则A等于( ).
(A)CBCT (B)C-1BC (C)CBC-1 (D)CTBC
三、(本题8分)在线性空间R4中,求由基ε1,ε2,ε3,ε4到基η1,η2,η3,η4的过渡矩阵,并求向量α=(1,0,0,-1)T在η1,η2,η3,η4下的坐标,其中
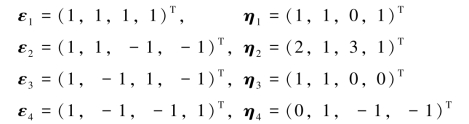
四、(本题10分)设C∈Rn×n,T是线性空间Rn×n中的如下的变换:
![]()
证明:(1)T是Rn×n中的一个线性变换;
(2)对Rn×n中的任意的X,Y,都有T(XY)=T(X)Y+XT(Y).
五、(本题10分)设α1,α2,…,αn是线性空间V中的一个基,按定义证明β1=α1,β2=α1+α2,…,βn=α1+α2+…+αn也是V中的一个基.
六、(本题10分)设R3中的线性变换为T(x1,x2,x3)=(x1+k1x2,x2+k2x3,x3).若R3中的向量α=(a1,a2,a3),β=(b1,b2,b3),η=(c1,c2,c3)线性无关,证明向量T(α),T(β),T(η)也线性无关.
七、(本题10分)设A∈Rn×n.(1)证明全体与A可交换的矩阵构成Rn×n的一个子空间,记为C(A);
(2)当A=E时,求C(A);
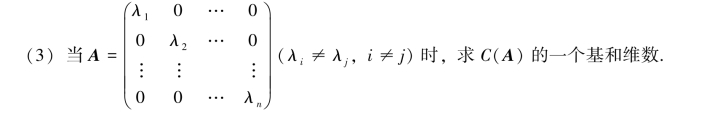
八、(本题12分)给定线性空间R3的两个基:
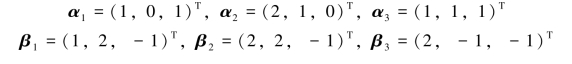
设T是R3中的线性变换,且
![]()
(1)写出由基α1,α2,α3到β1,β2,β3的过渡矩阵;
(2)写出T在基α1,α2,α3下的矩阵;
(3)写出T在基β1,β2,β3下的矩阵.
