1.6.1　行列式按行(列)展开定理

1.6.1　行列式按行(列)展开定理

首先,介绍余子式和代数余子式.

定义1.6.1　在行列式

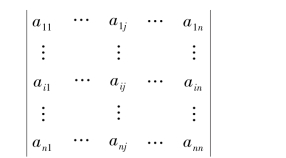
中划去元素aij所在的第i行与第j列,剩下的(n-1)2个元素按照原来的排列顺序构成一个新的n-1阶的行列式

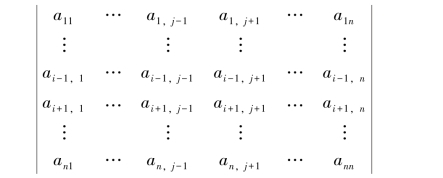
称为元素aij的余子式,记为Mij.记

称Aij为元素aij的代数余子式.

例1.6.1　试证明:

一般情形下,把第i行向下移动到第n行,共移动n-i次;然后把第j列移动到第n列,共移动n-j次;根据性质1.5.2,得

定理1.6.1　行列式等于它的任一行(列)的元素与其对应的代数余子式乘积之和.

证明　仅对行的情况进行证明.把行列式第i行的每个元素加n-1个0,由行列式性质1.5.8,分成n个行列式之和,即有

对于复杂的高阶行列式,利用展开法则化简及计算行列式的前提是某行(列)有很多零元素或者利用行列式的性质化简成某行(列)有很多零元素.