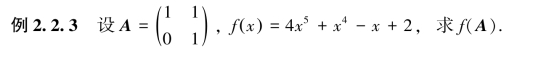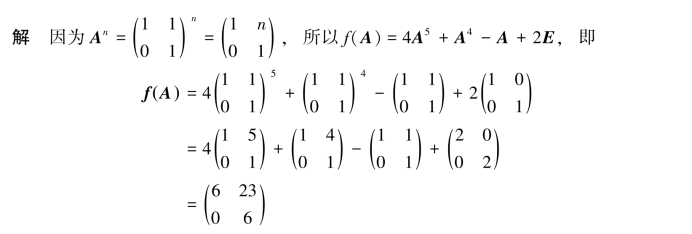2.2.3 矩阵与矩阵相乘
设有两个线性变换:
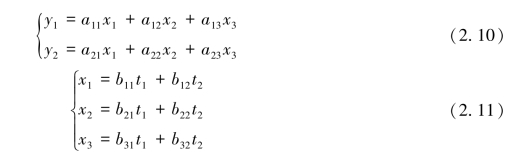
若想求出从t1,t2到y1,y2的线性变换,可将式(2.11)代入式(2.10),便得到
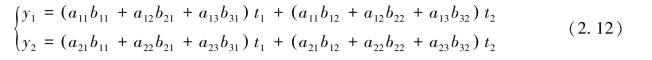
线性变换(2.12)可看成先作线性变换(2.11)再作线性变换(2.10)的结果.我们把线性变换(2.12)叫作线性变换(2.10)与(2.11)的乘积,相应地把式(2.12)所对应的矩阵定义为式(2.10)与式(2.11)所对应的矩阵的乘积,即
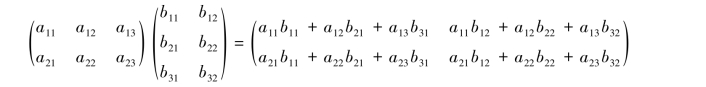
定义2.2.3 设A=(aij)m×s是一个m×s矩阵,B=(bij)s×n是一个s×n矩阵,则规定矩阵A与B的乘积是一个m×n矩阵C=(cij)m×n,其中
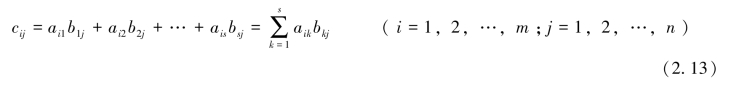
并把此乘积记作
注意:只有当第一个矩阵(左矩阵)的列数等于第二个矩阵(右矩阵)的行数时,两个矩阵才能进行乘法运算.
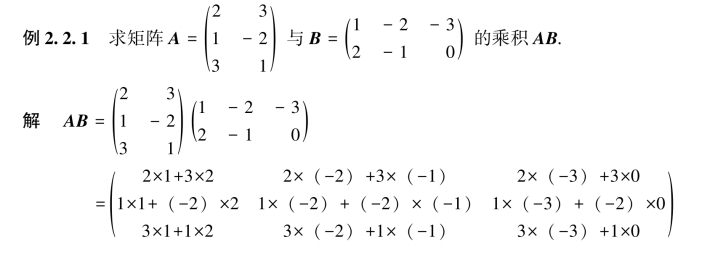
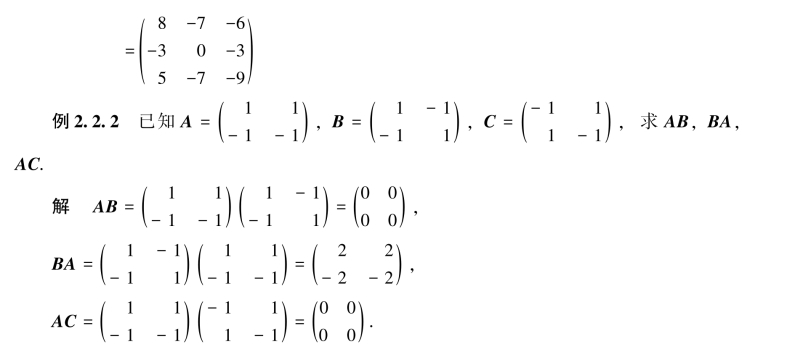
由例2.2.2可知,对于数的乘法成立的运算规律,对于矩阵的乘法并不都成立,值得提出的是以下三点:
(1)两个非零矩阵的乘积可能是零矩阵,反之,若AB=O,也不能得出A=O或B=O的结论;
(2)矩阵的乘法一般不满足消去律,即不能从AB=AC必然推出B=C;
(3)矩阵的乘法一般不满足交换律,即一般地,AB≠BA.特殊,对于同阶方阵A,B若满足AB=BA,则称其相乘是可交换的,比如
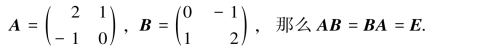
不过,矩阵的乘法仍然满足下列运算规律(假设运算都是可行的):
(1)(AB)C=A(BC);
(2)A(B+C)=AB+AC,(B+C)A=BA+CA;
(3)λ(AB)=(λA)B=A(λB)(其中λ为常数).
对于单位矩阵E,容易验证
可见,单位矩阵E在矩阵乘法中的作用类似于数1.
有了矩阵的乘法,可以定义矩阵的幂.设A是n阶方阵,则
其中k为正整数,即Ak就是k个A连乘.显然只有方阵的幂才有意义.
方阵的幂满足以下运算规律:
其中k,l为正整数.但是一般说来,(AB)k≠AkBk.
类似地,由于矩阵乘法一般情况下不满足交换律,因此数运算中的平方差、立方差、完全平方等公式都不再成立.
