3.7.4　基变换与坐标变换.

3.7.4　基变换与坐标变换.

下面讨论向量空间V的两个基之间的关系和同一向量在不同基下的坐标之间的关系.

设α1,α2,…,αn;β1,β2,…,βn是n维向量空间V的两个基.

令

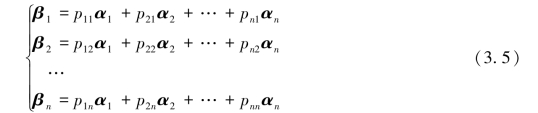
以βj(j=1,2,…,n)关于基α1,α2,…,αn的坐标为列可构成n阶矩阵:

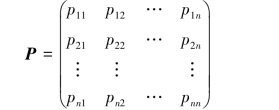
P称为由基α1,α2,…,αn到基β1,β2,…,βn的过渡矩阵.显然,任意一个基到自身的过渡矩阵就是单位矩阵E.

式(3.5)可以记作

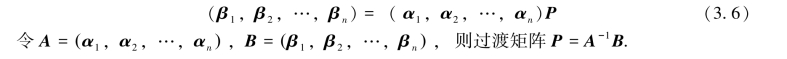
特别地,在n维向量空间Rn中取单位坐标向量组e1,e2,…,en为基,Rn中任一向量x=(x1,x2,…,xn)T在基e1,e2,…,en下的坐标为x1,x2,…,xn,e1,e2,…,en叫作Rn中的自然基.

例3.7.7　设R3的两个基Ⅰ和Ⅱ分别为

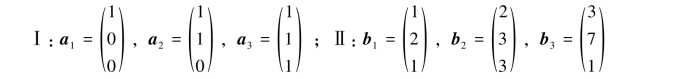
求由基Ⅰ到Ⅱ的过渡矩阵P.

解　由基Ⅰ到Ⅱ的过渡矩阵P=A-1B,其中A=(a1,a2,a3),B=(b1,b2,b3).用矩阵的初等行变换把矩阵(A,B)中的A变成E,则B相应地变成A-1B.计算如下: