本章小结

向量的线性相关性是线性代数的重点内容、也是难点内容之一,对逻辑推理能力要求较强,在学习时要深刻理解基本概念,搞清概念之间的相互关系,尤其要学会用定义作推导论证,推导中注意逻辑的正确性.

本章的研究对象是n维向量,学习过程中要深刻理解线性相关与线性无关的概念,掌握判定向量组线性相关性的常用方法;要理解向量组的秩和最大无关组的概念,理解矩阵的秩和向量组的秩之间的关系,会用矩阵的初等变换求向量组的秩和最大线性无关组;了解向量内积的概念和性质,掌握利用施密特正交化过程将线性无关的向量组规范正交化的方法以及正交矩阵的判别.在向量空间中,应在了解向量空间、向量空间的基、维数等概念基础上,会判定向量空间,会求向量空间的基、维数和向量的坐标,会求基变换、坐标变换.特别注意,向量由向量组的线性表示,向量组的线性相关性、向量在一个基中的坐标等问题都和方程组的解有密切的关系,解决这些问题的关键是要将其转化成线性方程组有解定理的等价条件.如向量b能由向量组A:a1,a2,…,an∈Rm线性表示也就是非齐次线性方程组Ax=b有解.向量组A:a1,a2,…,an∈Rm线性相关(无关),就是齐次线性方程组Ax=0有非零解(只有零解),即R(A)＜n(R(A)=n).

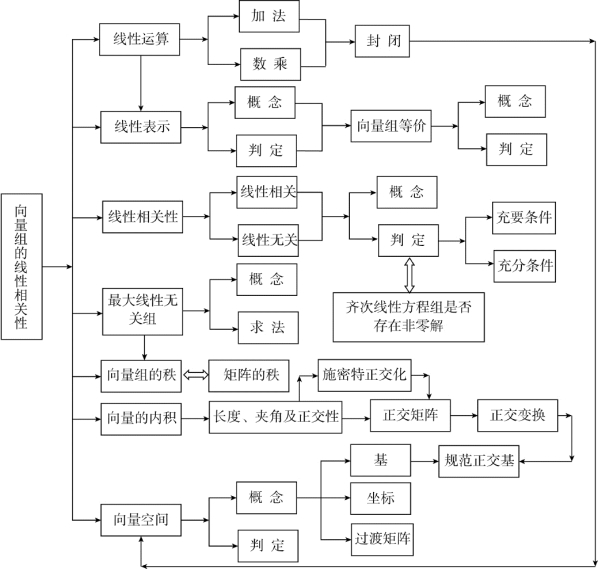
本章知识结构图如下: