5.7.2 二次型的定性概念及判定方法
定义5.7.1 设有实系数二次型f(x1,x2,…,xn)=xTAx,如果对于任意的x=(x1,x2,…,xn)T≠0,都有:
(1)f=xTAx＞0,则称f为正定二次型,并称实对称矩阵A是正定的;
(2)f=xTAx＜0,则称f为负定二次型,并称实对称矩阵A是负定的;
(3)f=xTAx≥0,则称f为半正定二次型,并称实对称矩阵A是半正定的;
(4)f=xTAx≤0,则称f为半负定二次型,并称实对称矩阵A是半负定的;
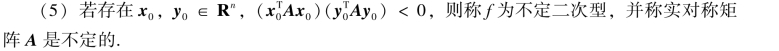
定理5.7.2 对于实系数二次型f(x1,x2,…,xn)=xTAx,下述命题等价:
(1)f是正定的;
(2)f的正惯性指数为n;
(3)A的特征值均大于零;
(4)存在n阶可逆实方阵B,使A=BTB.
定理5.7.3 对实对称阵矩阵A,下述命题等价:
(1)A是正定的;
(2)A的特征值全大于零;
(3)存在可逆实方阵B,使A=BTB;
(4)A与单位矩阵E合同.
推论5.7.1 若A是正定的,则det A＞0.
定理5.7.4 n阶对称矩阵A=(aij)n×n正定的充分必要条件是A的各阶顺序主子式都为正,即
而A负定的充分必要条件是奇数阶主子式为负,偶数阶主子式为正,即
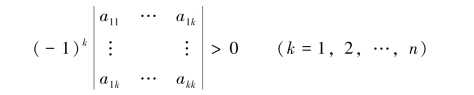
定理5.7.4叫作赫尔维茨(Hurwitz)定理,对于判定对称矩阵的正定性和负定性非常方便.
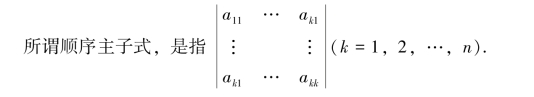
进一步,根据p的不同取值情况,对二次型矩阵有五种定性的描述:正定性、负定性、半正定性、半负定性和不定性.
推论5.7.2 实对称矩阵A正定、负定、半正定、半负定和不定的充分必要条件是A的特征值全为正数、全为负数、全部非负、全部非正和有正有负.
判断实二次型或实对称矩阵的正定、负定、半正定、半负定和不定的性质,在求多元函数的极值、二次曲线和二次曲面类型的判定、控制系统的稳定性分析等问题中,有重要的应用.
例5.7.1 判定二次型f(x,y,z)=-5x2-6y2-4z2+4xy+4xz的正定性.
解 f的矩阵为
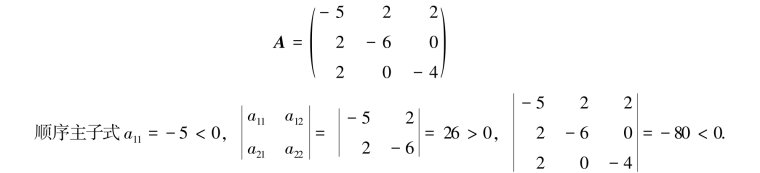
根据定理5.7.4,二次型f(x,y,z)=-5x2-6y2-4z2+4xy+4xz是负定的.
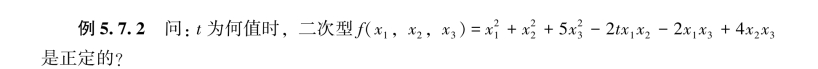
解 f的矩阵为
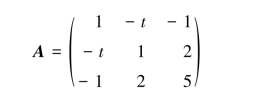
根据定理5.7.4,f正定的充要条件是顺序主子式全大于零,即
例5.7.3 证明:设n阶实对称矩阵A=(aij)n×n正定,则akk＞0(k=1,2,…,n).
证明 因为实对称矩阵A=(aij)n×n正定,即对任意非零向量x,总有xTAx＞0,取x=ek=(0,…,1,…,0)T≠0,有akk=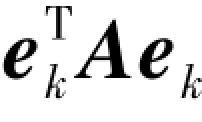
＞0.