1.6.2　利用按行(列)展开定理计算行列式

1.6.2　利用按行(列)展开定理计算行列式

例1.6.3　试证明:行列式中任一行(列)的元素与另一行(列)对应元素的代数余子式的乘积之和为零.

证明　仅对行的情况进行论证.也就是要证明:当i≠j时,ai1Aj1+ai2Aj2+…+ainAjn=0.

按第j行展开得

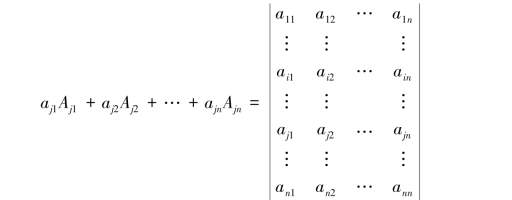
将第j行元素用第i行元素替换得

综合定理1.6.1和例1.6.3有如下公式:

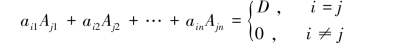
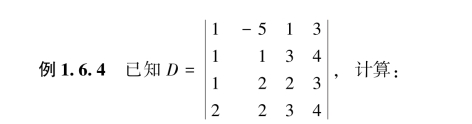
(1)A13+A23+A33+3A43;

(2)A21+2A22+2A23+3A24,其中Aij为元素aij的代数余子式.

解　(1)将第3列元素分别换成1,1,1,3,其余不动,再按第3列展开得

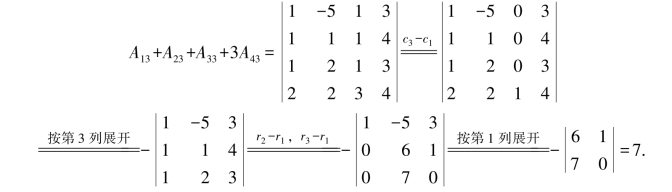
(2)A21+2A22+2A23+3A24相当于第3行元素与第2行对应元素代数余子式乘积之和,由例1.6.3知,结果为0.

例1.6.5　试证明:n阶范德蒙德(Vandermonde)行列式:

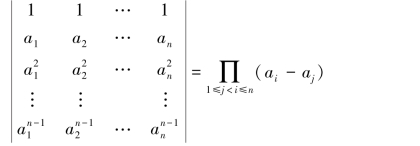
证明　对n应用数学归纳法.当n=2时,有(https://www.daowen.com)

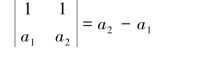
即n=2时命题成立.

假设对n-1阶范德蒙德行列式结论成立,则

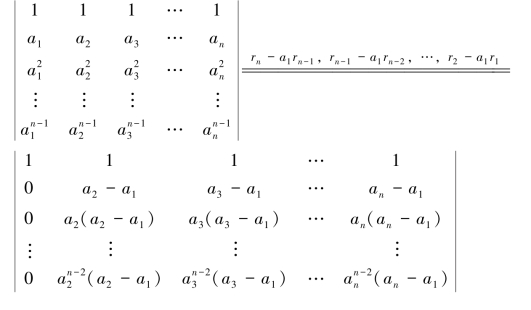
所以,结论成立.

例1.6.6　解方程:

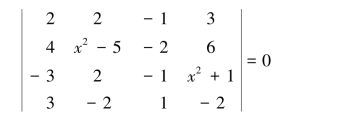
解　方程的左端是一个四阶行列式,先利用行列式的性质将其化为关于x的多项式,再求解方程.则

解得x=±1或x=±3.

例1.6.7　计算:

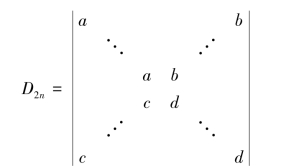
解　该行列式为2n阶,除了对角线有非零元素外,其余元素全为零.按第1列展开得

利用该递推公式可以计算行列式.