3.3.3　向量组的线性相关和线性无关的几何意义

3.3.3　向量组的线性相关和线性无关的几何意义

1.二维向量组的线性相关和线性无关的几何意义

在xOy坐标面上有向量组α,β,γ,若其中任意两个向量α,β线性相关,即共线,则α,β,γ必线性相关.设α,β线性无关,看看为什么向量组α,β,γ仍线性相关,如图3.2所示.

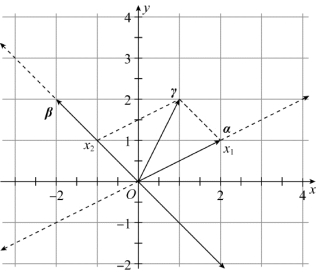
图3.2

图中向量α,β不在一条直线上,分别作过α,β的直线(如图中虚线所示),过向量γ的终点分别作α,β的平行线分别交α,β的直线于x1,x2(x1与x2距点O的距离分别为k1和k2),即得到向量γ的分解式γ=k1α+k2β.

改变向量γ的位置,仍然会得到同样的表达式,只是表达式的系数不同而已.因此,在平面上任意三个向量α,β,γ线性相关.

2.三维向量组的线性相关和线性无关的几何意义

这里只考虑向量组α,β,γ线性相关的情形.如果α,β线性无关,那么α,β会形成一个平面π:{k1α+k2β}.因为α,β,γ线性相关,所以γ必然会落在平面π上,即有γ=k1α+k2β,如图3.3所示.如果γ不落在平面π上,则α,β,γ线性无关,与α,β,γ线性相关矛盾.如果α,β线性相关,则α,β,γ必线性相关,如图3.4所示.

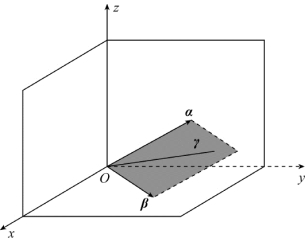
图3.3

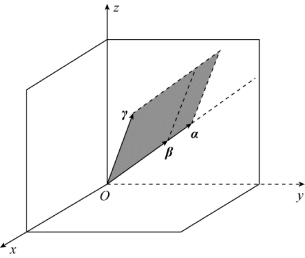
图3.4