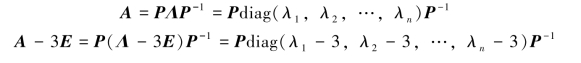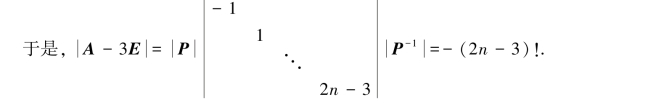5.2.2 方阵可相似对角化的充要条件
所谓矩阵的对角化,就是A能与一个对角矩阵相似.
定义5.2.2 若一个n阶方阵A与一个对角阵Λ=diag(λ1,λ2,…,λn)相似,就称A可以对角化.
我们知道,可以通过相似变换把A变成与特征值有关的最简单的形式.但是,并不是所有的方阵都能和最简单的对角矩阵相似.那么,在什么条件下矩阵可以对角化呢?要解决这个问题,矩阵的特征值和特征向量起着重要的作用.
定理5.2.2 n阶矩阵A与对角阵相似(即A能对角化)的充分必要条件是A有n个线性无关的特征向量.
证明 必要性.设矩阵A与对角阵相似,则存在可逆矩阵P,使P-1AP=Λ=diag(λ1,λ2,…,λn),于是,AP=PΛ.
设P的第i列向量为pi,即P=(p1,p2,…,pn),则有
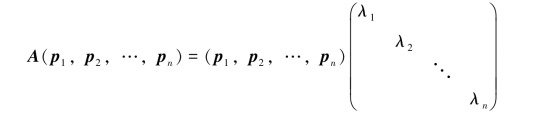
根据矩阵的分块乘法及矩阵相等的定义,得Api=λipi(i=1,2,…,n).
因此,λi是A的特征值,pi就是A的对应于特征值λi的特征向量.根据P的可逆性可知,p1,p2,…,pn线性无关;
充分性.设A有n个线性无关的特征向量p1,p2,…,pn,依次与特征值λ1,λ2,…,λn相对应,根据特征值的定义式,有Api=λipi(i=1,2,…,n).
令P=(p1,p2,…,pn),则P是可逆矩阵,记Λ=diag(λ1,λ2,…,λn),则

于是,P-1AP=Λ=diag(λ1,λ2,…,λn),即矩阵A与对角阵相似.
因为特征向量不是唯一的,所以矩阵P也不是唯一的,并且还可能是复数矩阵.(https://www.daowen.com)
本章例5.1.2和例5.1.3都是特征方程有重根的情形.其中,例5.1.2的特征重根对应一个线性无关的特征向量,也就是A只有两个线性无关的特征向量;而例5.1.3的特征重根对应两个线性无关的特征向量,也就是A有三个线性无关的特征向量,因此,例5.1.2中的矩阵A不能对角化,例5.1.3中的矩阵A因为有三个线性无关的特征向量而可以对角化.
当A的特征方程有重根时,就不一定有n个线性无关的特征向量,也就不一定能对角化.

得λ1=-1,λ2=λ3=1.
对应单根λ1=-1,可求得线性无关的特征向量恰有1个,故矩阵A可对角化的充分条件是对应重根λ2=λ3=1,有2个线性无关的特征向量,即方程(A-E)x=0有2个线性无关的解,亦即系数矩阵A-E的秩R(A-E)=1.
化A-E为行阶梯形矩阵,即
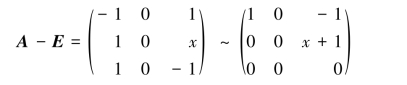
要使R(A-E)=1,即x+1=0,得x=-1.
因此,当x=-1时,矩阵A能对角化.
推论5.2.3 如果n阶矩阵A的n个特征值互不相等,则A与对角阵相似.
![]()
解 因为A有n个互异的特征值,根据推论5.2.3,A与对角阵相似,存在可逆矩阵P,使P-1AP=Λ=diag(λ1,λ2,…,λn).根据推论5.2.2知,λ1,λ2,…,λn是A的特征值,所以有