6.3.2 线性变换的矩阵表示式
定义6.3.3 设T是线性空间Vn中的线性变换,在Vn中取定一个基α1,α2,…,αn,如果这个基在变换T下的像为
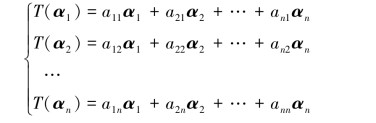
记T(α1,α2,…,αn)=(T(α1),T(α2),…,T(αn)),则上式可表示为
![]()

这样,在Vn中取定一个基后,由线性变换T可以唯一地确定一个矩阵A,由一个矩阵A也可唯一地确定一个线性变换T.故在给定基的条件下,线性变换与矩阵有一一对应的关系.
由关系式(6.4)可知T(α)在基α1,α2,…,αn下的坐标为
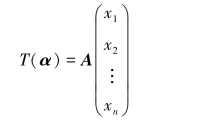
即按坐标表示有T(α)=Aα.
例6.3.4 在线性空间R2×2中定义线性变换T如下:
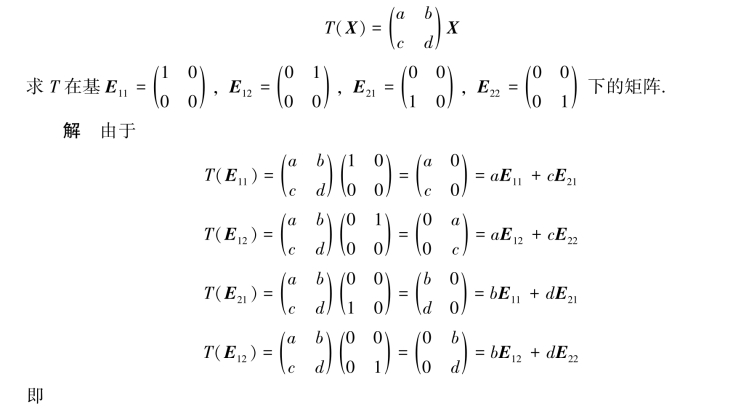

例6.3.5 在R3中,取基i=(1,0,0),j=(0,1,0),k=(0,0,1),T表示将向量投影到xOy平面的线性变换,即
![]()
(1)求T在基i,j,k下的矩阵;
(2)取基为α=i,β=j,γ=i+j+k,求T在该基下的矩阵.(https://www.daowen.com)

由此例可见:同一个线性变换在不同的基下一般有不同的矩阵.那么这些矩阵之间有什么关系呢?
定理6.3.3 设线性空间Vn中取定两个基α1,α2,…,αn和β1,β2,…,βn,并且由基α1,α2,…,αn到基β1,β2,…,βn的过渡矩阵为P,Vn中的线性变换T在这两个基下的矩阵依次为A和B,则B=P-1AP.
证明 由已知
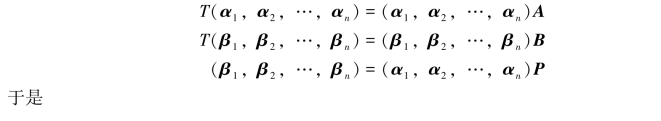
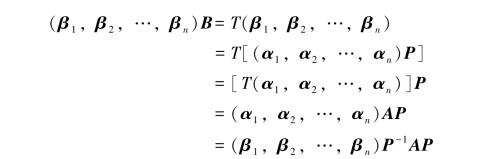
因为β1,β2,…,βn线性无关,所以B=P-1AP,即B与A相似,且两个基之间的过渡矩阵P就是相似变换矩阵.

定义6.3.4 设V是实数域R上n维线性空间.
![]()
称T是V的数乘变换.那么T关于V的任意一个基下的矩阵是

特别地,V的单位变换关于任意一个基下的矩阵是单位矩阵;零变换关于任意一个基下的矩阵是零矩阵.
这样,在取定一组基之后,就可以建立由实数域R上n维线性空间V的线性变换集合L(V)所构成的线性空间到数域R上的n×n矩阵集合Rn×n所构成的线性空间的一个映射.这个映射是一一对应关系.
定理6.3.4 实数域R上n维线性空间V的所有线性变换构成的线性空间L(V),在取定基之下,与数域R上的n×n矩阵集合所构成的线性空间Rn×n是同构的,从而dimL(V)=dim Rn×n=n2.
