2.6.3　秩的性质

2.6.3　秩的性质

下面讨论矩阵的秩的性质:

(1)0≤R(Am×n)≤min{m,n};

(2)R(AT)=R(A);

(3)若A~B,则R(A)=R(B);

(4)若P,Q可逆,则R(PAQ)=R(A);

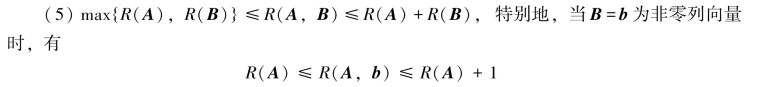
证明　由于A的最高阶非零子式也是(A,B)的非零子式,于是R(A)≤R(A,B),同理有R(B)≤R(A,B),从而有

从而有

(6)R(A+B)≤R(A)+R(B);

证明　不妨设A,B为m×n矩阵.对矩阵(A+B,B)施行初等列变换ci-cn+i(i=1,2,…,n),得

于是有

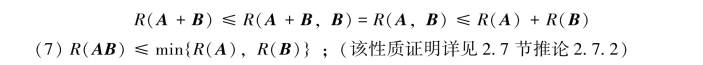
(8)若Am×nBn×t=O,则R(A)+R(B)≤n.(该性质证明详见4.1节例4.1.2)

例2.6.6　设A为n阶矩阵,证明R(A+E)+R(A-E)≥n.

证明　由于(A+E)+(E-A)=2E,由矩阵的秩的性质(6)可知

又由于R(E-A)=R(A-E),于是有

例2.6.7　证明:若Am×nBn×t=C,且R(A)=n,则R(B)=R(C).

当矩阵的秩等于它的列(行)数时,称矩阵为列(行)满秩矩阵.当矩阵为方阵时,列(行)满秩矩阵就成为满秩矩阵,即可逆矩阵.因此,当例2.6.7中的矩阵A为方阵时,结论就是矩阵的秩的性质(4).

在例2.6.7中,当C=O时,结论变为:若AB=O,且A为列满秩矩阵,则B=O.